2023年前半のよかったもの/微妙だったもの
最近技術メモとかは他媒体に移行しており、あまりモチベはないが思ったことの供養として書く。
良かったものたち
外食
外食全然やってないので自由が丘の京城苑を勧めるためだけに項目を書いた。
- ランチ1800円弱でお肉もご飯も爆盛。しかも超旨い。
- ランチは予約出来ないっぽいので1時間弱並ぶかもしれない。が、それでも全然また行きたい。
- 複数人の客だけでなく結構一人でビール片手に焼肉食っている人もいるのでその点気楽かもしれない。
水天宮の近くにある百名店のうどん屋もまた行きたい。
冷凍食品
最近の冷食はめっちゃ美味しい。が、特に感動したのを挙げるとこんな感じ。
改悪されないことを祈る。
- セブンのピザ
- 550円と冷食にしては高いが全然店で出るレベルのピザ。うまい。
- Ease upのイタリアン雑炊
- 基本的にヨーカドーのEase Upはどれもうまいがこれが一番好き
- トマト味の旨辛海鮮リゾットという感じ。サンフランシスコでCioppinoとか食べたことあればあれが一番近いと思う

飲料
- Fanta レモンプレミア ピンクグレープフルーツ

ガジェット
最近あまり新しく買ってないが使っていて良いと思ったものは下記の通り。
- Huawei Band 7
- 程よいサイズ感と何より電池が10日以上保つのが良すぎる(睡眠計測・LINE通知などを主に使用)
- その他スマートウォッチに必要な基本的な機能はほぼついている
- Huawei製品であるという点以外は完璧👍
- Atom Cam2 (Swing)
- 監視カメラ・見守りカメラとして購入
- 暗所でもはっきり見える、アプリからなら外出先から色々操作できる
- 非公式のハッキングも充実: Github repo
- いろいろやってるとSDカードを壊してしまう可能性はあるらしい。遊びがいのある良いガジェット。
これとか参考になる。 ATOM Cam 2 / ATOM Cam Swing で atomcam_tools を試してみたメモ - Qiita
- AnkerのAC充電器
- PCのACアダプタがでかすぎてうんざりしていたが、これでかなり省スペース化できた。
- 100Wに対応するケーブルも買わないといけないのでそこだけ注意。
微妙だったものたち
普段は書かないが、供養してくれという気持ちがあるので書く。
モバイルディスプレイ
仕事部屋の空調の効きがあまりに悪いため、他の部屋でも仕事できるようにLenovoのThinkVisionというモバイルディスプレイを買った。
頑張って箇条書きで書こうとしたが、結局サブディスプレイに求めるのは広いワークスペースなので解像度が低いディスプレイでは満足できないということが言いたい。 有象無象メーカーでも同価格帯なら4Kのディスプレイがあるのでそちらを試したい。というか部屋で使うならコンパクトな据え置きのディスプレイでいい気がする(バッテリーを内蔵しているガジェットの管理に困っているので)
- 良かった点
- 自立機構や接続周りなど、作りはしっかりしている。一応モバイルディスプレイとしては十分使える。
- コンパクトで比較的軽量なので出張先とかに持っていく分には結構良さそう。
- 微妙な点
- 圧倒的な解像度不足。正直開発用のサブディスプレイとしては1920x1080は狭すぎる。
- USB-C電源からパススルーで接続できるが、ケーブル数が減るわけではないので正直不要な機能だと感じた。
アウトドア椅子
これはモノはいいが運用に困るという話で、近くの河原に持って行って何度か使ったが正直屋外で組み立てる手間がだいぶだるかったので全然使わなくなった。私がものぐさなだけかもしれないが外に出てPCや本を読むという行為が定着したら評価が変わるかもしれない。
あと意外とかさばる。来客時にでも出そうか。
こっちの製品はDランドに行くときに活躍したが普段遣いで必要な場面は微塵もない。畳んで場所を取らない分上記の椅子よりは良いかも。
【備忘録】結婚式でフォトコンテストをした時の設定事項メモ(LINE APIとGooglePhoto API使用)
最近全くブログを書くモチベがないですが,昔やった/できたことを完全に忘れるのは忍びないので備忘録だけでも放流しておきます。
基本的には技術的なメモを書くので運営的な反省については書かない予定。
フォトコンテストをする際に参考にしたもの
下記のブログを参考にLINE botとGooglePhotoの連携を試した。
Heroku上にサーバーを立ててそこからLINE APIとGooglePhotoAPIを叩いてLINE BOTとGooglePhotoをつなぐ形式である。
元記事のソースコードはいくつか挙動が合わなかったので改変したVerを自分のGithubにて管理している。
Heroku側の設定
Heroku上でのConfig設定
アクセストークンなどの値は直接サーバーにあげずにconfig値として送ると多少セキュアらしい。
heroku config:set <NAME>=<VAL>
.envファイルでまとめて入れても良い。 https://blog.44uk.net/2019/03/16/heroku-config-multiple-set-and-remove/
その場合は下記のコマンドでセットできる(bash限定)
heroku config:set $(cat .env)
DOSのコマンドプロンプトからは下記のどちらかを叩いた気がする。
FOR /F "usebackq" %i IN (`type env_heroku.txt`) DO heroku config:set %i FOR /F "usebackq" %i IN (`type .env_heroku`) DO set %i
Heroku上でのコミット設定
以下を参照
データベースURIってなんだっけ?
Flask初めてだったので上記の疑問がメモに残っていた。
データベースの記述フォーマットのことで
dialect+driver://username:password@host:port/database名みたいな形式で書くらしい。
ここでは面倒だったので
DATABASE_URI=sqlite:////tmp/photocontest.db
とした。
db/photocontest.sqliteでも良かったかも。
ngrokでデバッグ
heroku上でデバッグするのはちょっとしんどかったのでローカル上でデバッグするためにngrokというのを使った。
ローカルからwebhookのURLを獲得することができる。いろいろ初期設定したら下記を叩くだけだった。
ngrok http 5000
GooglePhotoやGoogleの認証まわり
Googleの認証周りはとにかく面倒だった。正直今でも何もわかっていない。
Credentialsを取得するPythonスクリプト
Googleの管理画面でアプリ用のIDとSECRETを取得した後,実際のAPIを叩くためにはCredentialsというものを取得しなければならない。
これが意外と面倒なのでスクリプトで一気にできるようにした。下記を適当なファイルで保存して実行すればOK。
- input: 同じフォルダに
client_id_secret.jsonが必要 - output:
credentials.jsonができる
# google_photos.py import google.oauth2.credentials import google_auth_oauthlib.flow import json import os from datetime import datetime, date from matplotlib.pyplot import get #from googleapiclient.discovery import build from verify_reflesh_token import verify_credentials, get_accesstoken_from_refreshtoken SCOPES = ['https://www.googleapis.com/auth/photoslibrary'] API_SERVICE_NAME = 'photoslibrary' API_VERSION = 'v1' CLIENT_SECRET_FILE = 'client_id_secret.json' CREDENTIAL_FILE = 'credentials.json' def support_datetime_default(o): if isinstance(o, datetime): return o.isoformat() raise TypeError(repr(o) + " is not JSON serializable") def getNewCredentials(): flow = google_auth_oauthlib.flow.InstalledAppFlow.from_client_secrets_file( CLIENT_SECRET_FILE, scopes=SCOPES) credentials = flow.run_console() with open(CREDENTIAL_FILE, mode='w') as f_credential_w: f_credential_w.write(json.dumps( vars(credentials), default=support_datetime_default, sort_keys=True)) return credentials def getCredentials(): if os.path.exists(CREDENTIAL_FILE): with open(CREDENTIAL_FILE) as f_credential_r: credentials_json = json.loads(f_credential_r.read()) credentials = google.oauth2.credentials.Credentials( credentials_json['token'], refresh_token=credentials_json['_refresh_token'], token_uri=credentials_json['_token_uri'], client_id=credentials_json['_client_id'], client_secret=credentials_json['_client_secret'] ) valid = get_accesstoken_from_refreshtoken( credentials_json['_client_id'], credentials_json['_client_secret'], credentials_json['_refresh_token']) print("Credentials is ", credentials.valid, valid) if not valid: print("Credential is Old!") credentials = getNewCredentials() else: print("Credential is not found!") getNewCredentials() return credentials def main(): credentials = getCredentials() # service = build( # API_SERVICE_NAME, # API_VERSION, # credentials=credentials # ) if __name__ == "__main__": main()
Credentialsが有効か確かめるスクリプト
上記で取得したCredentialsはすぐ有効期限が切れるのでこれが有効かどうか手っ取り早く試す作業もスクリプト化した。
- input :
credentials.json - output: Credentialsが有効化どうか文が出力される
# google_photos.py import requests import json import google CREDENTIAL_FILE = "credentials.json" def load_credential_file(): with open(CREDENTIAL_FILE) as f_credential_r: credentials_json = json.loads(f_credential_r.read()) credentials_dict = { "client_id": credentials_json["_client_id"], "client_secret": credentials_json["_client_secret"], "refresh_token": credentials_json["_refresh_token"] } return credentials_dict def verify_credentials(credentials): client_id = credentials["client_id"] client_secret = credentials["client_secret"] refresh_token = credentials["refresh_token"] token = get_accesstoken_from_refreshtoken( client_id, client_secret, refresh_token) if token: print("Credentials is valid. Gained access token is:", token) return True else: print("Credentials is not valid!") return False def get_accesstoken_from_refreshtoken(client_id, client_secret, refresh_token): params = { "grant_type": "refresh_token", "client_id": client_id, "client_secret": client_secret, "refresh_token": refresh_token } authorization_url = "https://oauth2.googleapis.com/token" authorization_url = 'https://www.googleapis.com/oauth2/v4/token' r = requests.post(authorization_url, data=params) if r.ok: return r.json()['access_token'] else: # 失敗したときにRequestを表示 print("Failed to get Access token!", r) return None def main(): credentials = load_credential_file() verify_credentials(credentials) if __name__ == "__main__": main()
アップロードできない!?
後に気づいたことだがどうもAPIで作ったアルバムじゃないとAPIからアップロードできない仕様になっているっぽい。 ここがGooglePhotoを結婚式のフォトコンテストに一番勧めにくい点である。私のケースではCredentialsが万が一にも切れないよう,当日の朝にHerokuにPushして運用した。
https://www.sukerou.com/2020/10/gapino-permission-to-add-media-items-to.html
LINE まわり
本当に何もメモが残っていないので多分苦戦しなかったものと思われる。 多分なにかに使ったコードがあるのでメモする。
- なんか秘密鍵・公開鍵を作るときに使ったプログラム
from jwcrypto import jwk import json key = jwk.JWK.generate(kty='RSA', alg='RS256', use='sig', size=2048) private_key = key.export_private() public_key = key.export_public() print("=== private key ===\n"+json.dumps(json.loads(private_key),indent=2)) print("=== public key ===\n"+json.dumps(json.loads(public_key),indent=2))
- private_keyを読んでJWTを出すプログラム。何に使ったっけ?
import jwt from jwt.algorithms import RSAAlgorithm import time import json with open("privatekey.txt", 'r') as json_open: privateKey = json.load(json_open) headers = { "alg": "RS256", "typ": "JWT", "kid": "d173551d-2f74-4faa-81af-5ae3eb545c0a" # your key } payload = { "iss": "1657287856", # channel ID "sub": "1657287856", # channel ID "aud": "https://api.line.me/", "exp": int(time.time())+(60 * 30), "token_exp": 60 * 60 * 24 * 30 # token valid sec } key = RSAAlgorithm.from_jwk(privateKey) JWT = jwt.encode(payload, key, algorithm="RS256", headers=headers, json_encoder=None) print(JWT)
スキャンしたレシートをGoogle Vision APIを使って自前でOCRしてcsv形式に変換する(Python)
はじめに
概要
レシートをScanSnapでスキャンした画像を
Google Vision APIを使ってOCRして
Pythonを使ってzaimに渡せるようなcsv形式に変換してみた
問題提起
家計管理のため、レシートをzaimという家計管理アプリでスキャンして管理しているのですが自分は定期的に撮影するということができず、200枚近くのレシートをためてしまいました。
これらの写真を撮影して...という作業に嫌気が指したのでScanSnapでまとめてスキャンしてOCRも自前でできたらいいなということで作業をはじめました。
Google Vision APIについて
Pythonで軽く試せるOCRにはいくつか選択肢があります。
前回Tesseraactを使って見た感想として、チューニングなどしないときちんと精度が出ず結構面倒だったというのがあったので
すでにある程度完成しているGoogle Vision APIというものを使ってみました。
レシートOCRに関しては下記の記事がちょうど該当したのでこちらを流用してOCRしていこうと思います。
実際の処理
本来は下記のようなデータフローを想定しています。
画像 -> OCR結果 -> 辞書型などのデータ -> csv形式
しかし、Google Vision APIが従量課金制である都合上OCRをかける回数を最小にしたいため、JSONファイルを介して結果を保存して再利用します。
(最初だけ行う) 画像 -> OCR結果 -> JSONファイル (試行錯誤する処理) JSONファイル -> 辞書型などのデータ -> csv形式
画像のOCRと保存
別記事に書いたのでそちらを参照してください。
について書いてあります。
OCR結果を使いやすい形式に変換
下記を流用します。
- 概要:行ごとにOCR結果のテキストをまとめる
- 入力:OCR結果のオブジェクト
- 出力:データのリスト
- 処理
- テキストと位置に関する記述を抽出
- テキストのBoundingBoxの左上の縦方向位置(Y座標)によってテキストをクラスタリング
以降ではこの関数を通して作成したlinesというリストを前提とします。
def get_sorted_lines(response,threshold = 5): """Boundingboxの左上の位置を参考に行ごとの文章にParseする Args: response (_type_): VisionのOCR結果のObject threshold (int, optional): 同じ列だと判定するしきい値 Returns: line: list of [x,y,text,symbol.boundingbox] """ # 1. テキスト抽出とソート document = response.full_text_annotation bounds = [] for page in document.pages: for block in page.blocks: for paragraph in block.paragraphs: for word in paragraph.words: for symbol in word.symbols: #左上のBBOXの情報をx,yに集約 x = symbol.bounding_box.vertices[0].x y = symbol.bounding_box.vertices[0].y text = symbol.text bounds.append([x, y, text, symbol.bounding_box]) bounds.sort(key=lambda x: x[1]) # 2. 同じ高さのものをまとめる old_y = -1 line = [] lines = [] for bound in bounds: x = bound[0] y = bound[1] if old_y == -1: old_y = y elif old_y-threshold <= y <= old_y+threshold: old_y = y else: old_y = -1 line.sort(key=lambda x: x[0]) lines.append(line) line = [] line.append(bound) line.sort(key=lambda x: x[0]) lines.append(line) return lines
必要なテキストの抽出
最低限必要なテキストとして重要な順に下記が挙げられます。
- 日付
- 店名
- 金額
- 品目名(Optional)
これらについてそれぞれOCR結果を用いて抽出をしていきます。 思ったよりも手順が莫大になってしまったので詳細は個別記事に書きました。
日付の抽出
日付は正規表現を使うことで文字列から抽出できると考えて実装しました。
大まかにはそれで良かったのですが、OCRの都合で年や月といった文字が認識されていなかったりしたのでそういう意味では苦労しました。
店名の抽出
店名は基本的に最初の方にデカデカと載っているため下記の手順を考えました。
- 上から5行分の文字列を抽出
- その中から最も縦方向に大きなBoundingBoxを持つものを店名とする
上記は正直必ずしも正しくない方針ですが、ある程度店目に検討が付けばよいと思い強行しました。
金額の抽出
金額は基本的に「小計」または「合計」というキーワードと対応している...と思いましたが思ったよりも様々な表記がなされていて、フローがとても複雑になってしまいました。
OCR結果のcsv形式への変換
さて、最後はZaimにOCR結果をCSVでアップする段ですが、下記のように項目ごとに列を指定できるので普通のcsv形式に変換しちゃって良さそうです。

Pandasでちょちょっと書けば終わりなのと後述の理由もあってやる気をなくしたので省略させてください。
オチ
散々いろいろやって気づいたのですがZaimは有料会員にならないとカテゴリをcsvから読んでくれません。
ということでこれではカテゴリの管理ができません…。アホかと…。
一応、それっぽくまとめたものを下記においておきます。
ffmpegを使ってDVDの動画をmp4でPCに保存(要ImgBurn)
はじめに
DVDから動画を抽出したい人けどなんかステマみたいな記事ばかり乱立しているし変なソフトを入れさせられたくない…
ということで手元にあるソフトでなんやかんやした結果できましたよという報告です。
なお,ImgBurnだけはDVDへの書き込み・読み込みどちらでも使えるので許してください。
この界隈は下記の記事のようにフラットに比較や説明をする体で自サイトのソフトを勧めるように誘導するサイトがなんかやたら多く感じます。
用意するもの
- Windows10
- ImgBurn : ISOファイルへの変換に必要
- ffmpeg:mp4への変換に必要
ffmpegもImgBurnもインストールが済んでいるものとします。
手順1:DVD->ISOファイルへと変換
DVDをドライブに差し込んだあと,ImgBurnをつけると下記のようなメニューが出ます。

中央左の「Create Image From Disk」をクリックするとDVDの中身をISOファイルへと変換してくれます。
手順2:ISO->mp4変換
下記に詳細があります。
差し込んですぐ再生される系のDVD(イベントものでもらえるDVDなど)の場合はコマンドは簡単で
ffmpeg -i <your file>.iso <output>.mp4
とすれば良いです。
以上!
Adobe Premiere系のソフトが起動しなくなった時にやったこと(Windows10)
サポートコミュニティに投稿すべきな気もしますが質問投稿サイトっぽいレイアウトだったのではてなに放流します。
概要
結論: Creative Cloudをアンインストールして入れ直したら全てうまく行った。
症状と対策
- Adobe Premiere ProとRushがどちらも起動しなくなった。タスクマネージャーのプロセスにも何故か出て来ない。
- アンインストールして入れ直そうにもアンインストーラーすらも起動しない。
- Creative Cloudにも同様の問題があったのでアンインストーラーをダウンロードしてアンインストール
- Creative Cloud側から諸ソフトを起動するとちゃんと起動した
Adobe公式にはCreative Cloudのアンインストールは慎重に的なことが書いてありますが,今回の件ではまぁしょうがないでしょう。
参考にしたリンク
まずは公式のリンクを見るべきです。ただ,私のケースではプロセスも立ち上がらなかったので役に立たなかったわけですが。
露骨なアフィリエイトが入ってはいるが下記の手順もいくつか参考にしました。
ROS2の開発用にWindows Terminalを使ってbash/Powershellのタブ生成時に特定のbatを実行させる話(bashrc的な)
まとめ
- ROS2 みたいにターミナルを起動後に特定のコマンドを実行しておきたい場合の書き方のメモ
- ショートカットやWindows Terminalの起動時オプションに特定の記述を書くことで起動時に特定のプロセスを走らせられる
- 下記のような記法が使える
コマンドプロンプトの場合
# hogefuga.batを実行してそのまま開きっぱなしにする cmd.exe /k "hogefuga.bat"
Powershellの場合
# cmd1とcmd2を実行してそのまま開きっぱなしにする powershell.exe -NoExit -Command "cmd1.ps1; cmd2.ps1"
事例:ROS2でターミナル起動毎に実行する内容
今回の作業目的です。
ROS1でのsource devel/setup.bashに相当する作業がROS2でも必要です。下記チュートリアルを参照。
- コマンドプロンプトの場合
call C:\dev\ros2\local_setup.bat
- Powershellの場合
C:\opt\ros\galactic\x64\local_setup.ps1
上記コマンドをタブを開くたびに入力する必要があり面倒です。 (Powershellにはbashrcみたいなのがあるので実は不要ですが。)
他にもいろいろ設定する必要がありそう?な気がしますが,それは別の記事で検証します。
なんなら一つのファイルにまとめてからそれを実行すれば良いだけの気もしますしね。
補足: ROS2のインストール形式
ROS2のバイナリインストール時にはzipからではなく,aka.ms/rosに示されている手順でインストールしているため若干走らせているコマンドが異なる可能性があります。WindowsにWSLを経由せずにROS2を入れている人の母数が結構少ないのか情報が足りてないので分かり次第追記します。
Windows Terminalを用いた解決策
Windows TerminalはWSLやコマンドプロンプト,Powershellなどをまとめて扱えるMS公式のターミナルアプリです。 ここに下図のように呼び出したいターミナルソフトとその起動コマンドを設定することができるため,いちいち実行するのが面倒なコマンドを起動時に処理することができます。

新しいターミナルの登録手順
ここに新しくROS2用のコマンドプロンプト/Powershellのターミナル設定を登録します。
設定 -> 「新しいプロファイルの追加」から 「コマンドライン」 を使いたいターミナルソフトに応じて編集します。
コマンドプロンプトを用いる時の設定
コマンドプロンプトを用いる場合は下記のように登録すると良いです。(バージョンはgalacticの設定です)
cmd.exe /k "C:\opt\ros\galactic\x64\local_setup.bat"
/k の意味はbatファイルを実行後,プロセスをExitしないという意味です。
追記:その後なんやかんやあってfoxyに変更したのでコマンドは下記に変更しました。
cmd.exe /k "C:\opt\ros\foxy\x64\setup.bat && C:\opt\ros\foxy\x64\share\gazebo\setup.bat"
Powershellを用いるときの設定
Powershellでは下記のような記述を書くことによりROS2の設定を呼び出せます。
powershell.exe -NoExit -Command "C:\opt\ros\galactic\x64\local_setup.ps1"
なお,私はVisualStudioの設定も読ませた方がいいかなと思って下記を登録しています。長い...
powershell.exe -NoExit -Command "&{Import-Module """C:\Program Files (x86)\Microsoft Visual Studio\2019\Community\Common7\Tools\Microsoft.VisualStudio.DevShell.dll"""; Enter-VsDevShell 595a88d4 -SkipAutomaticLocation -DevCmdArguments """-arch=x64 -host_arch=x64""";C:\opt\ros\galactic\x64\local_setup.ps1}"
補足:複数のコマンドを実行したい場合
複数のコマンドを実行する必要性が出た場合は下記のようにすると良いです。
- コマンドプロンプトの場合:
&&で繋げる - Powershellの場合:
;で繋げる
参考にしたURLたち・免責
参考になったりならなかったりしたURLをおいておきます。
筆者が現時点でROS2の開発をフルにやっていないのでこれがおすすめ!とは言えないのであしからず。
windows — Linuxの.bashrcファイルに相当するウィンドウはありますか?
Safest way to run BAT file from Powershell script - Stack Overflow
Start-Process -FilePath """C:\opt\ros\galactic\x64\local_setup.ps1""" -Wait -NoNewWindow みたいな記法が書いてありましたが,これはちょっと期待していたのと動作が違ったのでパス。
3次元回転のオイラー角をそのまま補間したら駄目とは言うが実際どれくらい変わるのか?(Python)
はじめに
3次元回転にはオイラー角、回転行列、クォータニオン、ロドリゲスの回転公式と多岐に渡る表現方法があり、時と場合によってそれらを使い分ける必要があります。
中でも任意の2姿勢を補間する際、「オイラー角を始点と終端で補間するのは悪手で、代わりにLERPやSLERPを使うと良い」というのは教科書などに載っていて皆知っていると思いますが、一体どれほど悪くなるのかについて具体的に示した資料が見つけられなかったので自分でやってみました。
下準備
本題に入る前に下記について作成したものを載せておきます。
- python/matplotlibを用いた回転角の図示
- scipyを用いた3D回転の形式変換
matplotlibによる回転角の図示
入力した角度が三次元でどのような見た目になるかについて知りたかったので簡単にmatplotlibで表示できるclassを作りました。
回転順序は 1-2-3(x-y-z)の軸の順に回転する(R = RzRyRx)としました。
# 使い方 plane1 = Plane3D() plane1.rotate_points_123euler([10,20,20]) # degreeでroll pitch yaw角を入れる。 plane1.show_as_mesh()
こんな感じで回転された平面が図示されます。
import numpy as np import pandas as pd import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D import scipy from scipy.spatial.transform import Rotation as R class Plane3D: """ 3次元平面の描画用クラス """ def __init__(self, side_num=10): assert type(side_num) is int self.init_attitude(side_num) def show_as_mesh(self): # Create the figure fig = plt.figure() # Add an axes ax = fig.add_subplot(111,projection='3d') # plot the surface ax.plot_surface(self.__X, self.__Y, self.__Z) return ax def getXYZ(self): """ 保持している図示用の点群の座標を吐き出す関数 """ return self.__X, self.__Y, self.__Z def rotate_points_123euler(self,rpy): """ degree単位回転 1-2-3(x-y-z)の軸の順に回転する。すなわち R = RzRyRxを掛け算する。 """ R3d = self.euler2Robj(rpy) self.normal_vector = R3d.dot(self.normal_vector) self.calc_Z() def euler2Robj(self,rpy): """ degree単位回転行列の取得 1-2-3(x-y-z)の軸の順に回転する R = RzRyRxを返す """ R3d = R.from_euler('zyx',[rpy[2],rpy[1],rpy[0]],degrees=True).as_matrix() return R3d def set_points_123euler(self,rpy): """ 1-2-3(x-y-z)の軸の順のEuler角に姿勢を固定する """ self.normal_vector = np.array([0.,0.,1.0]).reshape(-1,1) self.rotate_points_123euler(rpy) def init_attitude(self,side_num): # ベースとなるGrid self.__X, self.__Y = np.mgrid[-side_num:side_num+1,-side_num:side_num+1] # 法線ベクトル(縦) self.normal_vector = np.array([0.,0.,1.0]).reshape(-1,1) # 高さ計算 dlen = side_num*2+1 self.__Z = np.zeros((dlen,dlen)) def calc_Z(self): if self.normal_vector[2,0] != 0: Z_ = - self.__X * self.normal_vector[0,0] - self.__Y * self.normal_vector[1,0] self.__Z = Z_ /self.normal_vector[2,0] else: print("Plane is Vertical!!")
ScipyのRotationの使い方について
ScipyのRotationにて1-2-3(x-y-z)の軸の順に回転する R = RzRyRxを返すには下記の書き方をする必要があります。この辺はパッケージによって違うので注意です。
個人的にはr-p-yの順に引数を与えたいと思ったのですが関数と仕様ケースが合わないのでLambda関数などを用いてごまかしています。
# RzRyRxの掛け算(Yaw-Pitch-Roll) R.from_euler('zyx',[y,p,r]).as_matrix()
ScipyのSLERPの使い方について
ScipyにはSLERP(球面補間)のライブラリが用意されています。 一見すると使い方がわかりにくかったのでこちらもメモしておきます。
from scipy.spatial.transform import Slerp rpy2ypr = lambda x: [x[2],x[1],x[0]] # slerp objectを生成 key_rots =R.from_euler('zyx', [rpy2ypr(rpy0), rpy2ypr(rpyn)], degrees = True) # 始点と終点 key_times = [0, 1] # 補間点を設定 slerp = Slerp(key_times, key_rots) # オブジェクト作成 # 0-1の間の補間点における角度をオイラー角で取得 slerp(0.4).as_euler('zyx',degrees=True)
オイラー角補間とSLERP(球面補間)の比較
ここではr-p-yが(0,0,0)と(10,20,30)または(20,40,60)の間で補間をしてみた際の違いを図示します。
SLERPで補間した結果をオイラー角に再度変換し直したものをオイラー角の線形補間と比較すると下図のようになります。
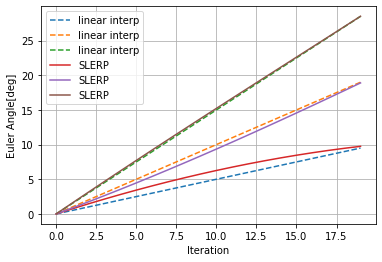
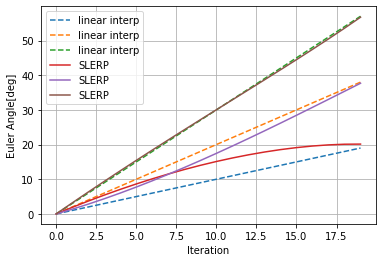
2点間の距離?が離れれば離れるほど差が顕著になるのがわかると思います。
このグラフを見て、結構違うなとなるかあんまり差がないなとなるかはアプリケーション次第だと思います。何か指標のようなものを知っている人がいたら教えて下さい。
ちなみに、もっとも差があるであろう補間の中央付近での3次元形状の違いを図示すると下記の様になります。
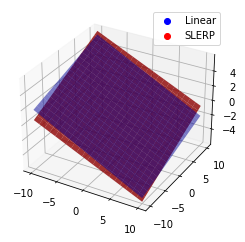
うーん、個人的にはあんまり変わらない気が... 角速度が重要なケースならよりSLERPの重要性が際立ちそうなものですが、以外と動かしてみたらバレないのではというのが筆者の所感です。 なにかCriticalなケースがあれば教えて下さい。
雑談
誤差状態カルマンフィルタ構築に向けたクォータニオンキネマティクス、という良さげな和文テキストが最近公開されました。ちょっと遊んで見ようかなと思っています。





