MATLAB 画像の相互情報量の計算と比較 (地図と航空写真のマッチング)

随分昔に遊んだコードを掘り出して懐かしくなったのでネットに放流します。
輝度値の二乗誤差（SSD)とはまた違う画像の相互情報量なるものを計算して画像を比較する手法の紹介です。
伝統的に医療用画像なんかのマッチングに使われている感じです。

今現在この手のコードは以下のリポジトリにて管理しています。
EvaluateImage/evaluate_image.m at master · YoshiRi/EvaluateImage · GitHub

Gist版はZNCCのコードに誤りがあります。（あとで直します）

相互情報量とは
- 画像の相互情報量
実際の比較：地図画像と航空写真のマッチング
実際のコード
参考論文

相互情報量とは

ある確率pで起こる事象の情報量Hは次のような式で表されます。
$H=\log_2 \frac{1}{p}=-\log_2p$

ある事象Aのもつ情報量をH(A)，BのをH(B)とすると，それらの間の相互情報量MI(A,B)は次の式で計算されます。
$MI(A,B)=H(A)+H(B)-H(A,B)$
ここで，H(A,B)はAもBも起こる時の情報量です。

画像の相互情報量

では，この話を画像に持ち込むとどうなるかといいますと，

事象：画像の中である画素値が出現する確率 p_I(i)とする。すなわち，0~255の画素値のうちxという画素がどの頻度で出現するかで先程の情報量を定義します。

画像Iの持つ情報量はIの中の全ての画素値の情報量の総和
$H({I})= -\sum_{i=0}^{N_{cI}} p_{{I}}(i)\log(p_{{I}}(i))$
として表され，これは実際の計算では出現回数を確率として正規化したヒストグラムを用意することになります。

同様にして結合情報は，
画像Iで画素がx，画像I*で画素がyとなる場合の2次元ヒストグラムを用いて同様に情報量を計算します。
$H({I,I^*})=-\sum_{i=0}^{N_{cI}} \sum_{j=0}^{N_{cI^*}} p_{{II^*}}(i,j) \log (p_{{II^*}}(i,j))$
注意として，例えば輝度を256階調にするとこのヒストグラムは256*256の結構大きな反復試行を要求されるので計算量が大きくなります。

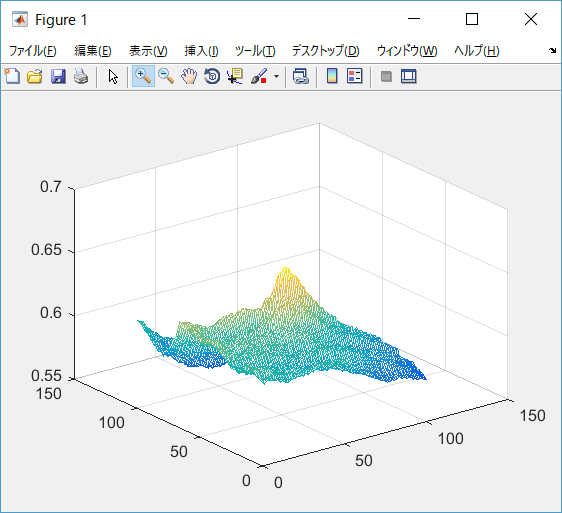
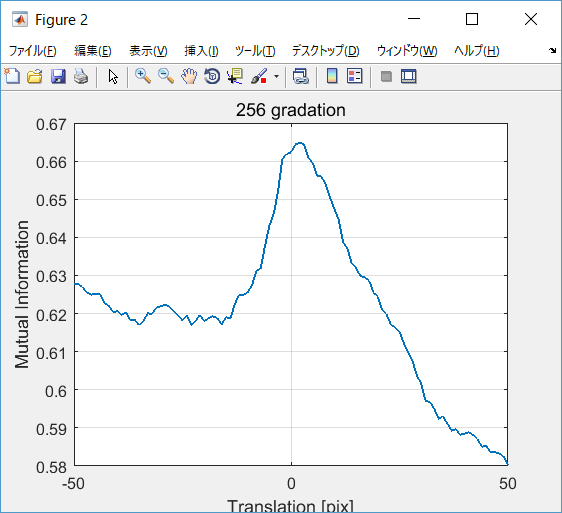
最終的に画像同士の相互情報量は以下の式で計算されます。
$MI({I,I^*})=H({I})+H({I^*})-H({I,I^*})$

この値が大きいほど，2つの画像の相関が高い，すなわちより似ていると評価できます。

実際の比較：地図画像と航空写真のマッチング

地図画像と航空写真をあわせるのは人間にはなんてことない作業ですが，
画像処理では画素値の相関が殆ど無いのでこれは結構きついです。

相互情報量はそのあたりなんとか出来るらしい[参考文献1]です。試してやんよ。

入力画像

航空写真 map_MI1
f:id:ossyaritoori:20161102140022p:plain

GoogleMapの地図画像 map_MI2c
f:id:ossyaritoori:20161102140029p:plain
を比較します。

結果の紹介

地図の画像を順次平行移動させながら，相互情報量を図っていくコードを組みました。

これが順次画像をずらしていった時の相互情報量のMappingです。
f:id:ossyaritoori:20161102132457p:plain

ここから，ある特定の地点で相互情報量が最大化されることがわかります。

わかりやすさのために，中心付近でx方向のみ切り出すと次のようになります。
f:id:ossyaritoori:20161102132550p:plain

ちょっとずれてるのが気になりますが，平行移動が0の時に航空写真と地図が最もマッチングしているということがわかります。
逆に言うと2つの画像のうち，片方の位置をずらして比較すると相互情報量が下がるということです。

比較手法

比較手法としてよくあるSSDとNCC，ZNCCを載せておきます。

f:id:ossyaritoori:20161212173607p:plain:w200 f:id:ossyaritoori:20161212173828p:plain:w200 f:id:ossyaritoori:20161212173917p:plain:w200

まぁあまり満足行く結果にはなりません。正直画像が悪すぎるというのもあるのですが。
とにかく相互情報量はこういった画像同士の相関を評価する手法として妥当そうという結論になります。

実際のコード

一年以上前に書いたのですごく汚いですが，
ご容赦ください。

コードを組む際のコツ：軽量化

説明の通り，ヒストグラムを作ってカウントアップしていくことで相互情報量を計算できるのですが，
普通の256階調でやると計算になかなか時間がかかります。

従って階調をダウンサンプリングすることでこの問題を回避できます。論文では8階調程度まで落としても平気そうと書いてありますね。

画像間の相互情報量を計算するコード

gradに階調を与えることで，軽量化を図っています。

比較手法のコード

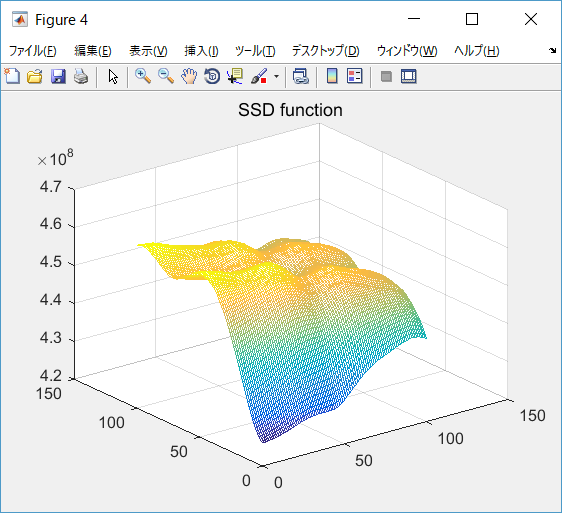
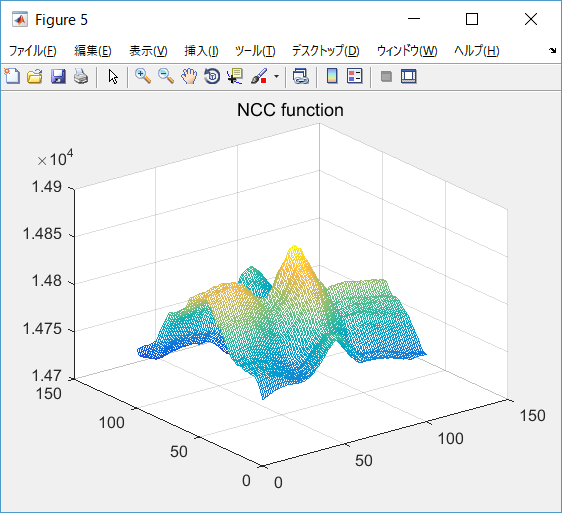
MIの比較用として，SSD，NCC，ZNCCを用いました。
まぁ説明なんかは下のサイトを見てください。教科書にあると思います。
パターンマッチング（正規化相関など）画像処理ソリューション

Gistに貼っておきました。お好きにどうぞ。

プロット用コード

上で述べた各関数を用いてプロットしています。
コツとしては移動させた時，画面外の領域を参照させないこと。
これをさせると存在しない領域との差を積み上げるため不確かな結果が出ます。

% Read image
AI = imread('map_MI1.png');
BI = imread('map_MI2.png');

% BI=imtranslate(AI,[15, -15]);

% if colored make it grayscaling
if numel(size(AI)) > 2
    AI = rgb2gray(AI);
end
if numel(size(BI)) > 2
    BI = rgb2gray(BI);
end


%% 
 MImap = zeros(101);
 
 for i = 1:101
     for j = 1:101
         Bii = imtranslate(BI,[i - 51, j - 51]);
         MImap(i,j)=MutualInformation(AI(51:205,51:205),Bii(51:205,51:205),16);
     end
 end
 
 %% find position
[mm,yy]=max(MImap);
[mv,mx]=max(mm);
my=yy(mx);
dx = mx -51;
dy = my -51;

% maximum value
MImap(my,mx)
BI_rev= imtranslate(BI,-[dx dy]);

figure(3)
imshow(imfuse(AI,BI_rev))
title('MI based matching')
 %% showing
 % mesh mapping
 figure(1);
 mesh(MImap);
title('MI function')

 
 memory = zeros(101,1);
 for i = 1:101
memory(i) = i-51;
 end

 % linear comparizon
 figure(2);
 plot(memory,MImap(51, :));
 grid on
xlabel('Translation [pix]');
ylabel('Mutual Information')
title('256 gradation');

 %% SSD ,NCC, ZNCC
  SSDmap = zeros(101);
  NCCmap = zeros(101);
  ZNCCmap = zeros(101);

  
 for i = 1:101
      for j = 1:101
          Bii = imtranslate(BI,[i - 51, j - 51]);
          SSDmap(i,j)=SSD(AI(51:205,51:205),Bii(51:205,51:205));
          NCCmap(i,j)=NCC(AI(51:205,51:205),Bii(51:205,51:205));
          ZNCCmap(i,j)=ZNCC(AI(51:205,51:205),Bii(51:205,51:205));
      end
 end

%% showing the results

figure(4);
 mesh(SSDmap);
 title('SSD function')

figure(5);
 mesh(NCCmap);
 title('NCC function')

 figure(6);
 mesh(ZNCCmap);
 title('ZNCC function')

参考論文

A. Dame, E. Marchand,'Second-Order Optimization of Mutual Information for Real-Time Image Registration'' IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 21, NO. 9, SEPTEMBER (2012)