MATLABでパーティクルフィルタ

流石に適当に書きすぎたか
この辺の分野はどの専門を土台にするかでかなり説明などが変わってきます。
私は制御＆ロボティクスが半々くらい。EKFやベイズの定理などはすでにMasterしているものとします。
（ていうか説明しない）

基礎は確率ロボティクスで勉強しよう。

確率ロボティクス (プレミアムブックス版)

ちなみに英語版のドラフトは以下のURLに落ちています。
https://docs.ufpr.br/~danielsantos/ProbabilisticRobotics.pdf
書籍版と比べましたが書籍版の方が洗練されてますね。英語読むの辛いし。

パーティクルフィルタとは

ベイズフィルタの亜種。状態推定に必要な確率分布を数式ではなく，多数の粒子群の集合として表現する手法です。
粒子の数を増やせば実質どのような分布でも表現でき，状態方程式とノイズの分布がわかっていればどのような関数でも同じように実装できるのが強み。

wikiを見るか以下の説明が簡潔かと。
なお，『カルマンフィルタもパーティクルフィルタも全部ベイズフィルタで説明がつく』という説明が美しいのでやはり上記の確率ロボティクスの本を読むことをおすすめします。
パーティクルフィルタ - おべんきょうwiki - アットウィキ

実装などについては以下のサイトが参考にしやすい。
Tutorial/Practice0 – MIST Project

Pythonの実装例でよければ確率ロボティクスを和訳した上田先生が公開しているモンテカルロ自己位置同定の話なんかが実装の参考になることでしょう。
github.com

後は鏡先生のスライドとかも参考になるか？
http://www.ic.is.tohoku.ac.jp/~swk/lecture/ic2012/kagami_ic20120710.pdf

matlab実装

というかMATLABの実装もAtsushiさんがやってくれてます。自己位置同定に関してはこれを使えば良いでしょう。
Particle Filterを使用した自己位置推定MATLABサンプルプログラム - MyEnigma

もう少し汎用的な話なら以下のブログがわかりやすいかと思います。式はいくつかこのブログから拝借してます。
satomacoto: Pythonでパーティクルフィルタを実装してみる

ちゃんとわかりたかったらやっぱり教科書を読みましょう。あれはやはり名著です。

各々の粒子は状態，重みをもつ。

状態推定

各々の粒子はそれぞれ自分の状態，重みをもつとします。

状態推定はEKF等と同じ流れで，状態方程式に基づいて各々の粒子を遷移します。
「各々のパーティクルごとに更新をするという点」と「実際に乱数を与えてノイズも加える」という点が少し違います。

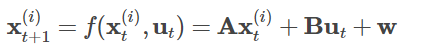
まぁモンテカルロって言ってますしね。実際に試していくわけです。

観測に依る更新

一方，状態更新の際には尤度を使って更新します。

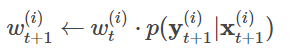
このp(Y|X)というやつが曲者ですが，ノイズをガウス分布と仮定するなら次のように書けます。
この更新に使う尤度は次のように計算します。（1次元の場合）

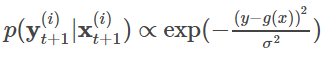
ここで，p(Y|X)は相対的な値がわかればよいです。
なぜなら，この後，全てのParticleに対して尤度を元に重みを更新しますが，更新した重みの和が1になるように正規化します。
従って，どうせ後で割り算でつじつま合わせの補正がされるので余計な計算はしなくて良いということですね。

ここが気味が悪いと思う人はやはり教科書を（ｒｙ
これもわかりやすく説明するのは他の人に投げたい。

個人的な解釈

解釈の例を載せておきます。間違っていたら指摘してください。

非線形出力方程式として
Y = g(X) ＋ ⊿
とでもしてみましょう。g()が非線形関数の出力で⊿が平均0，分散σ×σのガウス分布とします。
はてな形式で数式をうつのはだるいのでこれで勘弁

g(X)を左に移行する式変形をするとつまるところ，Y-g(X)は平均が0で分散がσ^2のガウス分布に従うことになります。
そしてガウス分布の式はWikiより次のように表せます。

このxの代わりにY-g(X)をぶち込んだ分布にXとYは従うということです。
つまり特定のXの時に特定のYを取る分布p(Y|X)はまさにこの分布に従うということです。
うーん，うーん，また教科書読み直してきます。
深夜に書いてて頭痛くなってきた。

リサンプリング

最後に新たに得られた重みの大きさに応じて粒子を再配置します。
パーティクルフィルタによる自己位置推定動作の可視化 - Qiita リサンプリングの項を参照。（孫引用で申し訳ない）

注意しないと確率の低めな粒子が全て淘汰されて推定値の集合が一点付近に収束してしまい，誤った値に収束して動けなくなったり，突然の外乱で値がずれたときに追従できなくなってしまうなどと言った問題が発生します。

これにも手法論がいろいろありまして
（確率ロボティクス第五回 参照）

「系統抽出法」を使うのがおおかた妥当らしいです。
重みを元に領域を区切り直して再びばらまく＆その際にランダム性を持たせて粒子の多様性を保存する的な意味合いです。

尤度の設定は重み付き平均でいいのか？

単峰性が確約されない場合重み付き平均は良くない場合も多いです。
以下のブログが非常にわかりやすい。
qiita.com

コード

応用例としてwikiの速度推定の話をしましょう。
カルマンフィルター - Wikipedia

速度がランダムウォークするとの仮定のもと，位置と速度の2つの状態を持つ状態を推定するという問題です。

コード置き場

例のごとくGistにあげました。リサンプリングとかはAtsusiさんのをほぼそのまま借りてます。ありがとうございます。

実装のコツ

クラスで作成しました。変数の状態等を内部できちんと管理するのにいいですね。
また，関数ハンドルとして状態方程式等を与えることに寄って，自分の設定した状態方程式に合わせた実装が容易にできるようにしました。
おそらく大体の関数においてこのコードは使用可能ではないでしょうか。

関数ハンドルにかんしては詳しくは「無名関数」でググってほしいですが

f=@(x,y)x+y

としたなら

f(x,y)
>> 5

という風に使えるものを関数ハンドルと呼びます。これで

state=@(x,u)A*x+B*u

とでも書けば状態方程式を簡単に定義できるというわけ。これは覚えて置いて損はないかと。

結果

なんかあんまり恩恵受けた感じしないですね。
とりあえず動いているのではなかろうか。

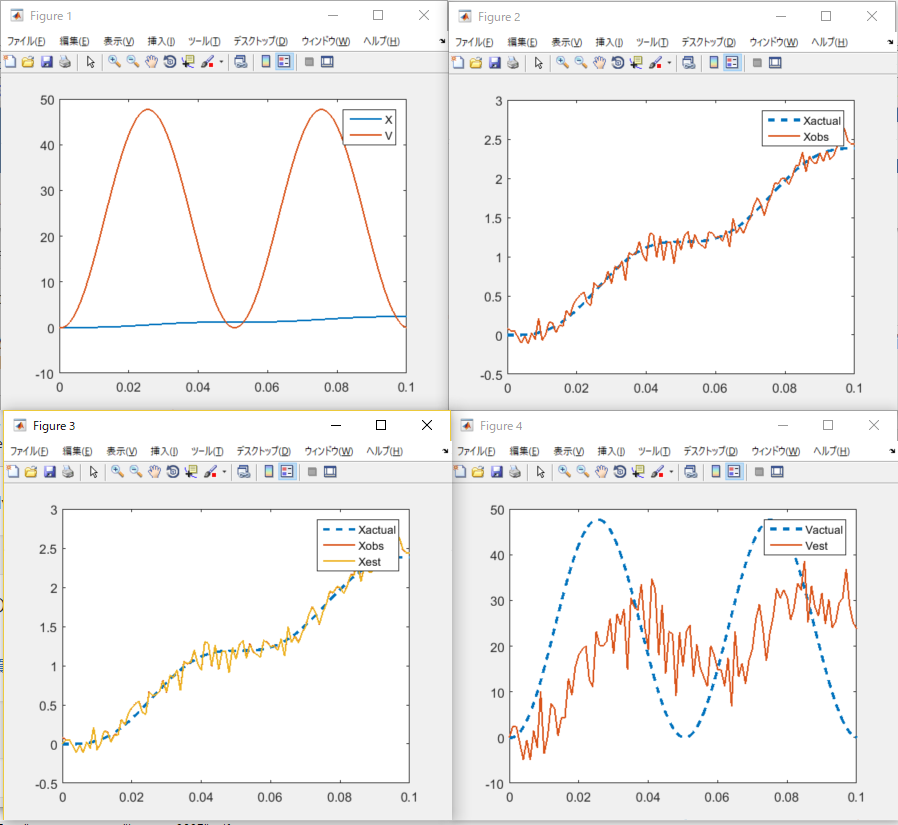
総評・所感

正直に言ってカルマンフィルタより実装が楽かというと全然そんなことは無いし，計算量もクソ重でした。
（これは行列演算ライブラリの利点を生かす実装をしなかったという点が大きいが）

一番困難なところはチューニングで，状態遷移のときのノイズをそれなりに大きく取らないとパーティクルがうまく撒けないし，
（追記：いや，これはどっちかというと初期値のバラまき方の問題というべきか。）
毎ステップでランダム要素が入るので，妙なことが起こるのではという不安もそれなりにあります。
そして周波数領域での設計とか超やりにくいじゃん！という致命的な制御屋の不満があったり，，，

何れにせよ多量のサンプルを用いて幅広い表現力を得た代わりにチューニングや設計のコツなども多分にややこしくなったというのが本当のところではないだろうか。

「パーティクルフィルタは簡単」との言はもっとロボットのローカライゼーションとかやる時に実感できるのかなぁ…