MatlabでLevenberg-Marquardt法 - 粗大メモ置き場

過去記事が地味に反応あったので調子乗って続きをば。
ossyaritoori.hatenablog.com

前回のGauss-Newton法に引き続き，
Levenberg-Marquardt法についてです。

フィッティングの手法としてはGauss-Newtonより多用される王道中の王道ですね。

概要
- アルゴリズムについて私的見解
- 知恵袋の秀逸な解答
問題設定
Gauss-Newton法との比較
- 補足：パラメータ空間でのアルゴリズムの様子
Levenberg-Marquardt法：コード
マッピングのコード

概要

前回のGauss-Newton法を前提にしているのでそっちを先に参照してくださいな。
matlabはstudentバージョンで2015aで動作します。
symbolic math Toolboxを使っております。

アルゴリズムについて私的見解

以下の記述は私の持ってるイメージですのであしからず。
間違ってたらコメントにて教えてください，

Gauss-Newton法は2次収束するNewton法において，ヘッセ行列をヤコビ行列の二乗で近似した手法ですが，
勢いが良すぎてぶっ飛んでしまうことがあります。
そこで，適切なダンピングファクターλを下のように導入します。

$\Delta v = - (J^TJ+\lambda I)^{-1}J^T \ r$

適度にダンピングをかけることで吹っ飛ぶのを回避できるってわけ。

なお，ダンピング項のIは最も簡単には単位行列，もう少し賢く行くにはヤコビアンの二乗の対角項を使うようです。
減衰最小二乗法とも言うようですね。

$\Delta v = - (J^TJ+\lambda diag(J^TJ))^{-1}J^T \ r$
matlabで書くならダンピング項はこんな感じか，簡単すな。

I = diag(diag(J.'*J))

知恵袋の秀逸な解答

なお，以下の知恵袋の解答も秀逸です。
Levenberg-Marquardt法（LM法）は非線形最小二乗問題を解く有力な... - Yahoo!知恵袋

「最急降下法とGaussNewton法の組み合わせ」という言はたしかにしっくり来ます。

以下の式は数学的には超間違い!!ですが，
感覚としてこんな感じってことなのはなんとなくわかります。
$\Delta v = - (J^TJ)^{-1}J^T \ r - \lambda^{-1} J^T \ r$

この式は怖い人がなんか言ってきたら消します（）

問題設定

前回のと同じ，wikipediaの例題です。
ガウス・ニュートン法 - Wikipedia

関数：
$y = \dfrac{ax}{x+b}$

Gauss-Newton法との比較

λをいじった場合どのように収束速度が変わるかを示す図が以下の通り。
f:id:ossyaritoori:20170201221137p:plain

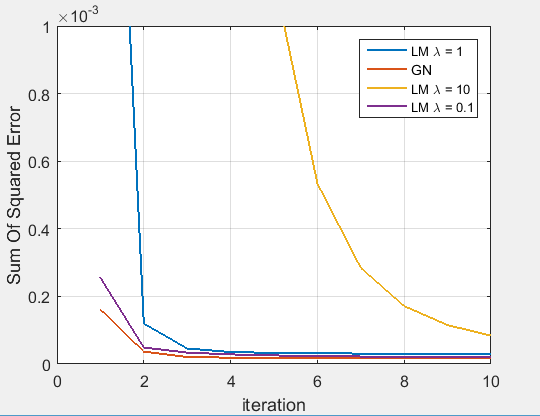
Legendが適当なのはごめんなさい。ダンピングと言う通り，λを大きくすると収束速度は鈍ります。

補足：パラメータ空間でのアルゴリズムの様子

変更するパラメータa,bを０～１の範囲で変えて残差の二乗和の関数の様子を見ました。

残差の二乗和： $S = \sum_{i=1}^n (r_i)^2$

f:id:ossyaritoori:20170201224437p:plain
なるほど今回の例では傾きの急な所から１方向にガツンと降りていくだけなのでそれほど差がないのも頷けます。
向かい側にも山があるお椀型の場合，GN法だと行ったり来たりする時がある印象です。

f:id:ossyaritoori:20170201225553p:plain
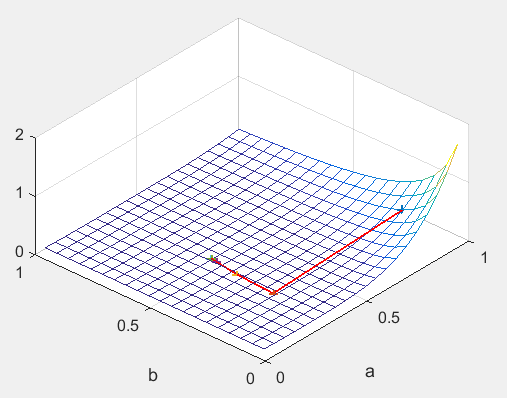
降りた時の軌跡はこんな感じ。我ながら結構わかりやすくなって満足。

Levenberg-Marquardt法：コード

基本的な解説はGaussNewton法の所を読んで下さい。
ダンピング項を加えただけです。

%%  https://ja.wikipedia.org/wiki/%E3%82%AC%E3%82%A6%E3%82%B9%E3%83%BB%E3%83%8B%E3%83%A5%E3%83%BC%E3%83%88%E3%83%B3%E6%B3%95
% http://org-technology.com/posts/gauss-newton-method.html

%% get data
clear all;
% data for fitting
xhat = [0.038, 0.194, 0.425, 0.626, 1.253, 2.500, 3.740].';
yhat = [0.050, 0.127, 0.094, 0.2122, 0.2729, 0.2665, 0.3317].';

%% making evaluate funciton
syms a b x y

% evaluate fuction
func = a*x/(x+b);
R = y - func;
S = R^2;

% partial derivative
Ra = diff(R,a);
Rb = diff(R,b);

% make jacobian matrix
Ja = subs(Ra,{x,y},{xhat,yhat});
% subs(fa,[x,y],[xhat,yhat]); ではダメ
Jb = subs(Rb,{x,y},{xhat,yhat});

Jacob = [Ja,Jb]; % jacobian


%% initial value
vinit = [0.9;0.2];
v = vinit;
iteration = 10;

% lambda
lambda = 1;
I = eye(size(Jacob,2));
% evaluate function
SumOfError = zeros(iteration,1);
SEF = subs(S,{x,y},{xhat,yhat});


%% iterative optimization
% error function
r = subs(R,{x,y},{xhat,yhat});

for i = 1:iteration
   J = double(subs(Jacob,[a,b],v'));
   df = double(subs(r,[a,b],v'));
   delta = - ( J.' * J  + lambda * I)\J.' *  df;
   v = v + delta;

   SOE = double(subs(SEF,[a,b],v'));
   SumOfError(i) = SOE.' * SOE;
end

%% showing
fit = subs(func,x,xhat);
yfit = double( subs(fit,[a,b],v') );

figure(3);
plot(xhat,yhat,'+',xhat,yfit);
xlabel('x');
ylabel('y');
legend('data','fitted value','Location','Best');
grid on;

figure(4);
plot(SumOfError);
xlabel('iteration');
ylabel('Sum Of Squared Error');
legend('Squared Error value')
grid on;

マッピングのコード

ndgridを初めて有効に使った気がします。
及第点。

%% mapping
Ms = 20;
Map = zeros(Ms);
% evaluate function
SEF = subs(S,{x,y},{xhat,yhat});
A = ndgrid(1:Ms,1:Ms)/Ms;
B = A.';


for i = 1:Ms
    for j = 1:Ms
        v = [i/Ms;j/Ms];
       SOE = double(subs(SEF,[a,b],v'));
       Map(i,j) = SOE.' * SOE;
    end
end

%% showing
figure(5);
mesh(A,B,Map);
xlabel('a');
ylabel('b');
grid on;