時間波形のsin波のゲイン・位相の変位を計算する（Python/Numpy）

概要
下準備：時系列データ作成
直交性を用いた解法
別解
余談：Cross-Correlationで位相計算にずれが生じる

概要

システム同定などのシチュエーションで単一のsin波を入力し、出力される波形とのゲインと位相差を計算したい場面があったので作成しました。

波形がSin波に似通っている＆周波数がわかっているならば直交性を用いた解法が良さそうです。

下準備：時系列データ作成

時刻の作成ではnumpyのarangeとlinspaceと仲良くなると良いです。

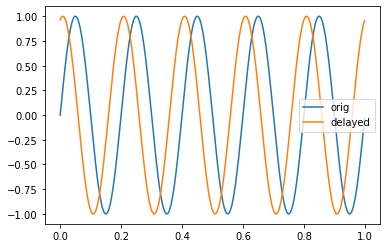
import numpy as np
import matplotlib.pyplot as plt


N = 1000            # 1000 sample data
sample = 0.001 # 1ms
freq = 5              # 5Hz


# 時刻作成
t = np.arange(0,sample*N,sample)
# 位相ズレ付きのSin波を作成する無名関数
x = lambda phi: np.sin(2*np.pi*freq*t+phi )

# 信号作成
y1 = x(0)
y2 = x(1.3) # 1.3 rad/s ずれたsin波

f:id:ossyaritoori:20220227183859p:plain

直交性を用いた解法

ゲインと位相を知りたい信号が $A sin(\omega t + \phi)$ とすると、 $cos(\omega t)$ と $sin(\omega t)$ の直交性から下記のような式が導けます。

$F_1(t) = cos(\omega t)A sin(\omega t + \phi) \\ = Asin(\omega t)cos(\omega t)cos(\phi)+Acos(\omega t)cos(\omega t) sin(\phi) \\ = \frac{A}{2} sin(2 \omega t) cos(\phi) + \frac{A}{2}(1 + cos(2\omega t) ) sin(\phi)$

この $F_1(t)$ を十分長い時間で平均すると、 $\frac{A}{2}sin(\phi)$ の項のみが残ります。

同様に $sin(\omega t)$ ともとの信号の各時間での値をかけ合わせた数値 $F_2(t)$ を十分長い時間で平均すると $\frac{A}{2}cos(\phi)$ が残るのでこれらを用いてゲインと位相が計算できる、という手法です。

def get_mag_and_phase(y,x):
    """
    y: input signal
    x: lamda function
    """
    cos_ = x(0)
    sin_ =  x(np.pi/2.0)
    N=len(y)
    a = sin_ * y
    b = cos_ * y
    A,B = a.sum()*2/N ,b.sum()*2/N
    
    mag = np.sqrt(A**2+B**2)
    phase = np.arctan2(A,B) 
    return mag, phase

def calc_mag_and_phase(y1,y2,freq,st):
    """
    input: 
            - y*: signal
            - freq_dot_t: frequency[Hz] * samplingtime [s]
    """
    N = len(y1)
    w = 2* np.pi* freq
    time = np.arange(0,N*st,st)
    x = lambda phi: np.cos(w*time+phi)
    mag1, phase1 = get_mag_and_phase(y1,x)
    mag2, phase2 = get_mag_and_phase(y2,x)
    
    
    return mag2/mag1, phase2-phase1

print(calc_mag_and_phase(y1,y2,freq,sample))

プログラム内では入力と出力の2つの信号の他に一度sinとcosの波を作ってそことの差分からゲインと位相差を計算しています。

これの明確な欠点として、下記の2つが挙げられます。

入出力の信号に無限時間平均で0にならないノイズがのっていると誤差が発生する
入出力信号の長さが周期の整数倍でないと誤差が発生する

前者はRANSACのような繰り返し処理による外れ値除去、後者は周期の整数倍になるように信号の時刻をCropする手が挙げられます。

後者に簡単に対応すると下記のような感じでしょうか。

def calc_mag_and_phase2(y1,y2,freq,st):
    """
    input: 
            - y*: signal
            - freq_dot_t: frequency[Hz] * samplingtime [s]
    """
    N = len(y1)
    w = 2* np.pi* freq
    t_max = np.floor(N*st)
    N_ = int(t_max/st)
    time = np.arange(0,t_max,st)
    x = lambda phi: np.cos(w*time+phi)
    mag1, phase1 = get_mag_and_phase(y1[0:N_],x)
    mag2, phase2 = get_mag_and_phase(y2[0:N_],x)
    
    return mag2/mag1, phase2-phase1

別解

下記サイトに様々な手法が載っています。上記の手法とどう違うのか式を追えてないのですが、

blog.goo.ne.jp

余談：Cross-Correlationで位相計算にずれが生じる

確か波形のズレを調べるだけならCross-Correlationから波形のズレが測れるはずだよな、と思い下記のコードを試してみました。

from scipy import signal

corr = signal.correlate(y1,y2,method='auto')
lags= signal.correlation_lags(len(y1), len(y2))
plt.plot(lags,corr)
amax = corr.argmax()
amin = corr.argmin()

print((lags[amax])*sample*2*np.pi*freq)

結果は 1.2566370614359172 となんとも惜しい値。相互相関の計算では時間軸上で-∞から+∞までの積分を想定しているため繰り返し数が足りないのでは、というお話でした。

stackoverflow.com

他にも位相相関も試してみましたが似たような問題で正しい値が出なかったので注意です。

def phase_corr(sig1,sig2):
    N = len(sig1)
    fft_sig1 = np.fft.fft(sig1)
    fft_sig2 = np.fft.fft(sig2)
    fft_sig2_conj = np.conj(fft_sig2)
    
    R = fft_sig1*fft_sig2_conj
    R/=np.absolute(R)
    r = np.fft.fftshift(np.fft.ifft(R).real)
    ar = np.unravel_index(r.argmax(), r.shape)
    
    plt.plot(r)
    return ar[0]-N/2, r[ar]