粗大メモ置き場

個人用，たまーに来訪者を意識する雑記メモ

RICOH THETA_SCで多重露光・合成をしてPixel4みたいにクリアな星空を撮りたい

Opencv Python コンピュータビジョン

この記事はたまたま集まった技術＆もの作りが好きな人たち Advent Calendar 2019の記事です。

はじめに

それはゴミのような論文を泣く泣く提出した日の夜でした。デスマを終えて見上げた空は信じられないくらい澄んでいてそれはもう最高に晴れやかな気分でした。

『こら撮らな！』と思いたって家からTHETAを引っ張り出してきて撮ったのが以下の写真です。

f:id:ossyaritoori:20191207235116p:plain
オリオンをなぞる。

何度かパシャパシャ撮ってから帰りましたが，やっぱり後でビューワーで視るとまだ少し物足りない感じがします。

そこで，Google Pixel4でも使われている多重露光を行って合成してより精細な写真を撮るという手法を試してみたくなりました。

以下がPixel4で撮った写真の一例らしいです。カッコよすぎんか。私も撮りたい。 https://image.itmedia.co.jp/news/articles/1910/17/ki_1609376_pixel4camera01.jpg

戦略

暗い夜空をきれいに取るためには露光時間を長くすればよいのですが，長すぎると星々が動いてしまいます。

Google Pixel4の戦略としては短めの露光を複数回撮って，それらを重ね合わせてノイズを除去しているようです。

japanese.engadget.com

ということで私も以下のような流れをとることにしました。

  • 360°カメラで星空を複数回撮影
  • 複数の画像を合成してノイズを落とす
  • 星空の回転に合わせて画像を補正

諸々の処理のプログラムはPythonで書きます。

Step0： 星空を撮る

撮影に使っているのはRICOHの全天球カメラのTHETA_SCです。

RICOH 360度カメラ RICOH THETA SC (ブルー) 全天球カメラ 910743

RICOH 360度カメラ RICOH THETA SC (ブルー) 全天球カメラ 910743

  • 発売日: 2016/10/28
  • メディア: エレクトロニクス

扱いやすく個人的には360度カメラの入門にはもってこいと思います。 撮像素子はデジカメでは標準的な 1/2.3型，レンズのF値は2.0とまぁまぁの明るさなので15秒程度露光すれば都心の夜空は十分に綺麗に撮れます。

都市郊外で空を撮る感覚だと 露光20-30秒 ，ISO：100-160程度が向いていそうです。

当日は小型の三脚に固定して撮影しました。

全天球カメラで撮った画像はEquirectalgular （正距円筒図法）という形式で保存されます。

f:id:ossyaritoori:20191208001928p:plain
スマホのパノラマで一周して撮ったときも同じような画像になりますね。


本稿ではこの画像の中心を原点とします。

横方向：水平方向へは一周で2π，縦方向は緯度方向なので一周でπのスケールがあります。 したがってざっくり画像座標→正距円筒座標の変換を書くと以下のようになります。

hei,wid,_ = image.shape
cx,cy = wid/2,hei/2
Equilecpoints = (np.array(polarpoints)-np.array([cx,cy]))/np.array([wid/2/pi,-hei/pi])

Step1：多重露光を合成する

ということで多重露光をした画像を合成する段階に入ります。 本来なら露光やISOを統一するべきなのですが，合成を思いついたのが撮影会後なので設定がバラバラな画像になってしまいました。

何も考えずにピクセル輝度の平均をとると以下のようにぼやけた画像になってしまいます。

f:id:ossyaritoori:20191210093417p:plain
建物と空の境界が曖昧に白っぽくなってしまう

そこでOpenCVにあるHDR合成（ハイダイナミックレンジ合成）のライブラリを使用してみることにしました。

HDR合成とは簡単に言うと露光条件の異なる画像を組み合わせて白飛び黒飛びを軽減した画像を撮像することです。

丁寧にまとめてくれている方がこちら（文献[1]）： [CV]High-Dynamic-Range(HDR) Imagingについて - Qiita

今回は最も楽そうなMergeMertensという手法を用いました。 Pythonで書くなら以下のような感じです。

import cv2
merge=cv2.createMergeMertens()
proc1 =merge.process([img1,img2,img3])

f:id:ossyaritoori:20191210112502p:plain
MergeMertensを用いた複数画像の合成結果


先ほどのようなモヤが生じる問題を回避できましたが，よく見ると星の動きが軌跡となっています。これはこれで乙ですがくっきりとした星空が見たいですね。

実際オリオン座の周辺に着目すると，星空が動いているのがよくわかります。

f:id:ossyaritoori:20191208001147g:plain
短い間にも空は動いている

露光を繰り返した3分強の間にも星々はよく動いていることがわかります。

Step 2 星空の回転を補正する

先程のGIF画像の様に星空は一日で天球を一回転します。回転中心は北極星（Polaris）近辺の極北にあたります。

OpenCVの既存関数による位置ずれ補正

OpenCVにもAlignMTBというクラスがあり，calculateShiftという関数で位置ずれを補正できるそうですがプログラムの中身を見た感じこれは微小並進量のみの対応です。

また，一般の平面画像であれば射影変換によって回転ズレを補正できます。 ossyaritoori.hatenablog.com

しかし，Equirectangular画像においては回転操作は非線形変換になります。

Equirectangular画像における三次元回転

回転操作がどの様に影響するか，次の座標変換から導出することができます。

f:id:ossyaritoori:20191210112100p:plain
3D直交座標と球面極座標の関係。文献[2]から引用

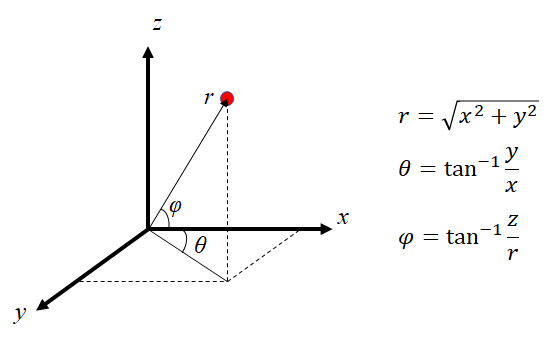
逆変換は以下の通りです。

\begin{align} x = cos \phi cos \theta, \\ y = cos \phi sin \theta, \\ z = sin \phi \end{align}

星空はrが変化しない無限遠にあるので，変換後のEquirectangular画像の \theta’,\phi’は天球上での三次元回転行列を用いて

\begin{pmatrix} x' \\ y' \\ z' \end{pmatrix} = R\begin{pmatrix} x\\ y \\ z \end{pmatrix}, \ \theta' = tan^{-1}\frac{x’}{y'} ,\ \phi'=sin^{-1}z'

と計算できます。

実際変形する際には (\theta’,\phi’)=(i,j)に対応する元画像の座標を逆変換から求め，ピクセル値をBilinear補間で求めます。

ロドリゲスの回転行列の計算

回転行列はOpenCVでサポートされているロドリゲスの回転行列を用います。


星空は原点と極北≒北極星を通る回転軸の反時計回りに回転します。1秒あたり1/240度なので微小のように思われますが，先程のGIFのように複数回露光をすると動きとして効いてきます。

変化を補正するために手動で極北の座標を決定した後，画像のExif情報から撮像の間隔を取得して回転変換をかけます。

# polarw ：Equirectangularでの極北のtheta,phi
nx = np.cos(polarw[1])*np.cos(polarw[0])
ny = np.cos(polarw[1])*np.sin(polarw[0])
nz = np.sin(polarw[1])

# omega = time_diff/3600/24*2*pi
Rrod,_ = cv2.Rodrigues(omega*np.array([nx,ny,nz]))

このRrodは先程の式における回転行列Rの転置になります。

変換＆重ね合わせの結果

ということで重ね合わせの結果です。

f:id:ossyaritoori:20191210161026p:plain
星空が合うようにマッチングしたので建物などがぶれて見える。

重ね合わせが成功して満足してしまいましたが，見えないものが見えるわけではないのでもっと暗い所に行って多重露光合成の威力を試したくなりました。 まずは休暇が欲しい…

STEP3 :自動で極北を抽出（途中）

SIFTやAKAZE特徴点でマッチングした画像は案の定，空と建物の境界にハマります。 星々をマッチングできれば回転を検出できますが，やはり空と建物・地面の分離を事前にやる必要がありそうです。

f:id:ossyaritoori:20191210212145p:plain
案の定有効な特徴点は空との境界に寄るため星空間の対応は難しそう。

夜空部分の抽出

先程のマッチングでは信頼度の低いマッチング結果を除去していました。具体的には距離情報で縛りをかけています。

良いマッチングを得るためにユークリッド距離の比を元に選別するコードがよく書かれています。

for m,n in self.matchings: 
   if m.distance < 0.75 * n.distance:
         #good.append()

この選別部分をなくした場合のマッチング点（AKAZE）はいくつか空の星々を捉えています。

f:id:ossyaritoori:20191213110200p:plain
青：画像1のAKAZE特徴点，オレンジ：画像2のAKAZE特徴点（マッチング実施後の対応点）

したがって，最初の選別有りのマッチングにて建物と空の協会となるY座標を抽出し，（今回はY=619）Y座標がその閾値以下，すなわちカメラから見てより上方にある箇所を空の領域と仮定しました。 その結果絞り込まれたのが以下の17点の対応です。

f:id:ossyaritoori:20191213112316p:plain
Y座標を元に夜空の部分の特徴点のみを抽出した

3次元座標での回転推定

Equirectangular平面内ではお互いの変換は非線形になってしまうので，一度求めた特徴点の対応を三次元球面極座標に写像してから対応する回転行列を求めます。

三次元回転の最適化といえば金谷先生の教科書を参照するのが良いでしょう。

3次元回転: パラメータ計算とリー代数による最適化

3次元回転: パラメータ計算とリー代数による最適化

また，一応英語のテキストが無料で転がっていたりします。

https://igl.ethz.ch/projects/ARAP/svd_rot.pdf

\sum Rx_i-y_iを最小化する回転Rは対応点x_iとy_iを列方向に並べた行列X,Yを用いて表した

S=XY^\topを特異値分解して得た U\Sigma V^\top=Sから，

\hat{R} = V diag(1,1,..,det(VU^\top)) U^\top

のように計算できます。なお，ここで推定したRはデータによっては厳密な回転行列にならない場合があります。それを補正するために同様の操作を繰り返します。 こちらは金谷先生の教科書に記述があるのでそちらを確認してください。

numpyでは以下のように書きます。np.linalgのsvdがVを転置の状態で出すことには注意です。

def estimate3dR(X,Y):
    S=np.dot(X,Y.T)
    U,W,V=np.linalg.svd(S)
    Rhat_ = np.dot(V.T,U.T)
    Rhat = np.linalg.multi_dot([V.T,np.diag([1,1,np.linalg.det(Rhat_)]),U.T])
    # additional Step For Optimization
    U,W,V=np.linalg.svd(Rhat)
    Rhat_ = np.dot(V.T,U.T)
    Rhat = np.linalg.multi_dot([V.T,np.diag([1,1,np.linalg.det(Rhat_)]),U.T])
    return Rhat

ランダムサンプルによるロバスト推定

ところで上記の手法でそのまま回転を計算すると，外れ値の影響を受けてしまいます。

この外れ値を除去するためにランダムサンプルによる手法が数多く提案されており，有名なRANSACなどはopenCVでの推定アルゴリズムにも採用されています。

二次文献ですが以下のブログがわかりやすいと思います。

www.sanko-shoko.net

RANSACの完全な実装はなかなかに面倒で，以下のブログを参考にしました。 クラスの継承を有効に使うコードを初めて書いた気がします。これはこれで長いので別記事で。

一目で分かるRANSAC - Qiita

その結果，

  • 手動設定の回転行列
array([[ 0.99989064, -0.00811519, -0.01236295],
       [ 0.00808042,  0.99996327, -0.00285925],
       [ 0.0123857 ,  0.00275904,  0.99991949]])
  • RANSACで推定した回転行列
array([[ 0.99994968, -0.00893819, -0.00455381],
       [ 0.00895058,  0.99995627,  0.00270865],
       [ 0.0045294 , -0.00274927,  0.99998596]])

はい。そこそこまともな値が抽出できてきました。 観測にノイズが混じっているのでこれは厳密には回転行列ではないので，補正が必要になります。（TODO:もう1つSubsectionが必要）

とりあえず，これをこのサイトにて分解して回転軸と回転角(rad)を抽出してみると，

[ -0.2625027, -0.4368636, 0.8603735 ], 0.0103961

これは，約143秒の露光という判定です…うーん，一分ほど短い？ 北極星の位置も微妙にずれた検出をしているのでマッチングの精度が悪かったかRANSACの調整ミスですね。（TODO）

また，回転中心の位置推定もやはり手動には敵いません。これはなかなか手ごわいです。

f:id:ossyaritoori:20191214002406p:plain
白：本来の北極星，黄色：自動推定した空の回転中心


とまぁこれ以上詳細に書くとめちゃ長くなるので別記事にします。 とりあえず，

  • 星空の領域抽出
  • 星空の運動の推定

がネックとなるため最初持っていたイメージよりかは簡単には自動化できないという感覚を得ました。 手動で北極星さえ指定すればExif情報で基本的に推定できるのでこの頑張りがそもそも必要かというのも少し怪しげですが気力があれば続きも記事にします。

TODO

  • 空の領域とそうでない領域の分離：雑にDone
  • 回転中心の自動抽出（特徴点マッチングを用いる）：雑にDone
  • 三次元回転推定まわりを整形：多分やる
  • 公開ようにプログラムを整形：やる？

おまけプログラム's

PILでgif画像を保存する関数

from PIL import Image
def saveasGif(images,filename='out.gif',duration=500,loop=0):
    imlist = []
    for img in images:
        img_array = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
        imlist.append(Image.fromarray(img_array))
        
    imlist[0].save(filename, save_all=True, append_images=imlist[1:], duration=duration,loop=loop)

Exifデータから撮影間隔を取得する関数

from PIL.ExifTags import TAGS
from datetime import datetime

# Exif データを取得
def get_exif_of_image(file):
    """Get EXIF of an image if exists.
    指定した画像のEXIFデータを取り出す関数
    @return exif_table Exif データを格納した辞書
    """
    im = Image.open(file)

    try:
        exif = im._getexif()
    except AttributeError:
        return {}

    exif_table = {}
    for tag_id, value in exif.items():
        tag = TAGS.get(tag_id, tag_id)
        exif_table[tag] = value
    return exif_table

def get_diff_time(file1,file2):
    """Calculate capture interval of images from  EXIF
    指定した2つの画像ファイル間の撮影時間の間隔を計算する
    """
    FMT = '%H:%M:%S'
    exif1=get_exif_of_image(file1)['DateTime']
    exif2=get_exif_of_image(file2)['DateTime']
    dtime = datetime.strptime(exif2[-8:], FMT) - datetime.strptime(exif1[-8:], FMT)
    return min(3600*24-dtime.seconds,dtime.seconds)

多くなりすぎたのでStep3に関しては別記事に移行する気がします。

参考文献等

[1] HDRなどに関して：[CV]High-Dynamic-Range(HDR) Imagingについて - Qiita

[2] 球面極座標に関する図表などの引用：360度パノラマ画像から平面画像への変換手法 - LASTMILE WORKS / DYNAMO TECH - R&D Project - Medium

[3] パノラマ画像から矩形画像を切り取るプログラム：GitHub - NitishMutha/equirectangular-toolbox: Handy tool for equirectangular images

他余裕でき次第追記