3次元回転のオイラー角をそのまま補間したら駄目とは言うが実際どれくらい変わるのか?(Python)
はじめに
3次元回転にはオイラー角、回転行列、クォータニオン、ロドリゲスの回転公式と多岐に渡る表現方法があり、時と場合によってそれらを使い分ける必要があります。
中でも任意の2姿勢を補間する際、「オイラー角を始点と終端で補間するのは悪手で、代わりにLERPやSLERPを使うと良い」というのは教科書などに載っていて皆知っていると思いますが、一体どれほど悪くなるのかについて具体的に示した資料が見つけられなかったので自分でやってみました。
下準備
本題に入る前に下記について作成したものを載せておきます。
- python/matplotlibを用いた回転角の図示
- scipyを用いた3D回転の形式変換
matplotlibによる回転角の図示
入力した角度が三次元でどのような見た目になるかについて知りたかったので簡単にmatplotlibで表示できるclassを作りました。
回転順序は 1-2-3(x-y-z)の軸の順に回転する(R = RzRyRx)としました。
# 使い方 plane1 = Plane3D() plane1.rotate_points_123euler([10,20,20]) # degreeでroll pitch yaw角を入れる。 plane1.show_as_mesh()
こんな感じで回転された平面が図示されます。
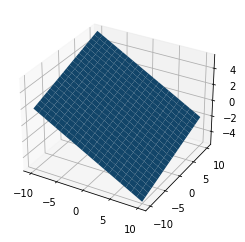
import numpy as np import pandas as pd import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D import scipy from scipy.spatial.transform import Rotation as R class Plane3D: """ 3次元平面の描画用クラス """ def __init__(self, side_num=10): assert type(side_num) is int self.init_attitude(side_num) def show_as_mesh(self): # Create the figure fig = plt.figure() # Add an axes ax = fig.add_subplot(111,projection='3d') # plot the surface ax.plot_surface(self.__X, self.__Y, self.__Z) return ax def getXYZ(self): """ 保持している図示用の点群の座標を吐き出す関数 """ return self.__X, self.__Y, self.__Z def rotate_points_123euler(self,rpy): """ degree単位回転 1-2-3(x-y-z)の軸の順に回転する。すなわち R = RzRyRxを掛け算する。 """ R3d = self.euler2Robj(rpy) self.normal_vector = R3d.dot(self.normal_vector) self.calc_Z() def euler2Robj(self,rpy): """ degree単位回転行列の取得 1-2-3(x-y-z)の軸の順に回転する R = RzRyRxを返す """ R3d = R.from_euler('zyx',[rpy[2],rpy[1],rpy[0]],degrees=True).as_matrix() return R3d def set_points_123euler(self,rpy): """ 1-2-3(x-y-z)の軸の順のEuler角に姿勢を固定する """ self.normal_vector = np.array([0.,0.,1.0]).reshape(-1,1) self.rotate_points_123euler(rpy) def init_attitude(self,side_num): # ベースとなるGrid self.__X, self.__Y = np.mgrid[-side_num:side_num+1,-side_num:side_num+1] # 法線ベクトル(縦) self.normal_vector = np.array([0.,0.,1.0]).reshape(-1,1) # 高さ計算 dlen = side_num*2+1 self.__Z = np.zeros((dlen,dlen)) def calc_Z(self): if self.normal_vector[2,0] != 0: Z_ = - self.__X * self.normal_vector[0,0] - self.__Y * self.normal_vector[1,0] self.__Z = Z_ /self.normal_vector[2,0] else: print("Plane is Vertical!!")
ScipyのRotationの使い方について
ScipyのRotationにて1-2-3(x-y-z)の軸の順に回転する R = RzRyRxを返すには下記の書き方をする必要があります。この辺はパッケージによって違うので注意です。
個人的にはr-p-yの順に引数を与えたいと思ったのですが関数と仕様ケースが合わないのでLambda関数などを用いてごまかしています。
# RzRyRxの掛け算(Yaw-Pitch-Roll) R.from_euler('zyx',[y,p,r]).as_matrix()
ScipyのSLERPの使い方について
ScipyにはSLERP(球面補間)のライブラリが用意されています。 一見すると使い方がわかりにくかったのでこちらもメモしておきます。
from scipy.spatial.transform import Slerp rpy2ypr = lambda x: [x[2],x[1],x[0]] # slerp objectを生成 key_rots =R.from_euler('zyx', [rpy2ypr(rpy0), rpy2ypr(rpyn)], degrees = True) # 始点と終点 key_times = [0, 1] # 補間点を設定 slerp = Slerp(key_times, key_rots) # オブジェクト作成 # 0-1の間の補間点における角度をオイラー角で取得 slerp(0.4).as_euler('zyx',degrees=True)
オイラー角補間とSLERP(球面補間)の比較
ここではr-p-yが(0,0,0)と(10,20,30)または(20,40,60)の間で補間をしてみた際の違いを図示します。
SLERPで補間した結果をオイラー角に再度変換し直したものをオイラー角の線形補間と比較すると下図のようになります。
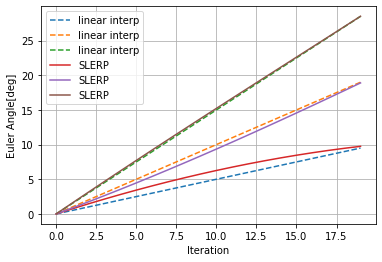
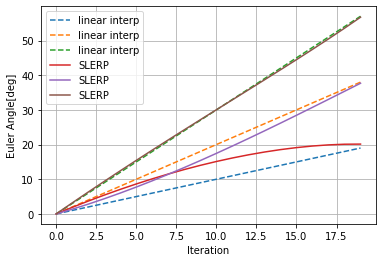
2点間の距離?が離れれば離れるほど差が顕著になるのがわかると思います。
このグラフを見て、結構違うなとなるかあんまり差がないなとなるかはアプリケーション次第だと思います。何か指標のようなものを知っている人がいたら教えて下さい。
ちなみに、もっとも差があるであろう補間の中央付近での3次元形状の違いを図示すると下記の様になります。
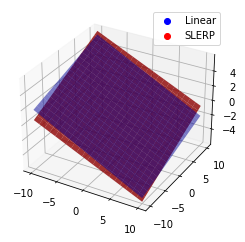
うーん、個人的にはあんまり変わらない気が... 角速度が重要なケースならよりSLERPの重要性が際立ちそうなものですが、以外と動かしてみたらバレないのではというのが筆者の所感です。 なにかCriticalなケースがあれば教えて下さい。
雑談
誤差状態カルマンフィルタ構築に向けたクォータニオンキネマティクス、という良さげな和文テキストが最近公開されました。ちょっと遊んで見ようかなと思っています。