モンテカルロ自己位置推定のテストとmatplotlibの覚書
こないだ千葉工大の上田先生の講演を聞いてきました。
そうです。あの「確率ロボティクス」を翻訳した方です。

確率ロボティクス (Mynavi Advanced Library)
- 作者: Sebastian Thrun,Wolfram Burgard,Dieter Fox
- 出版社/メーカー: マイナビ出版
- 発売日: 2015/04/02
- メディア: Kindle版
- この商品を含むブログを見る
はじめてお会いしましたが,講演もフランクで親しみやすそうという印象でした。
Python環境のセットアップ
先日書いた記事はこれに相当します。
ossyaritoori.hatenablog.com
コピペで実行。
確率ロボティクスではロボットが自身の位置に対する信念を「制御」と「観測」の値から推定しながら動くわけですが,
その最たる例が今回のMCL(Monte Carlo Localization)というわけです。
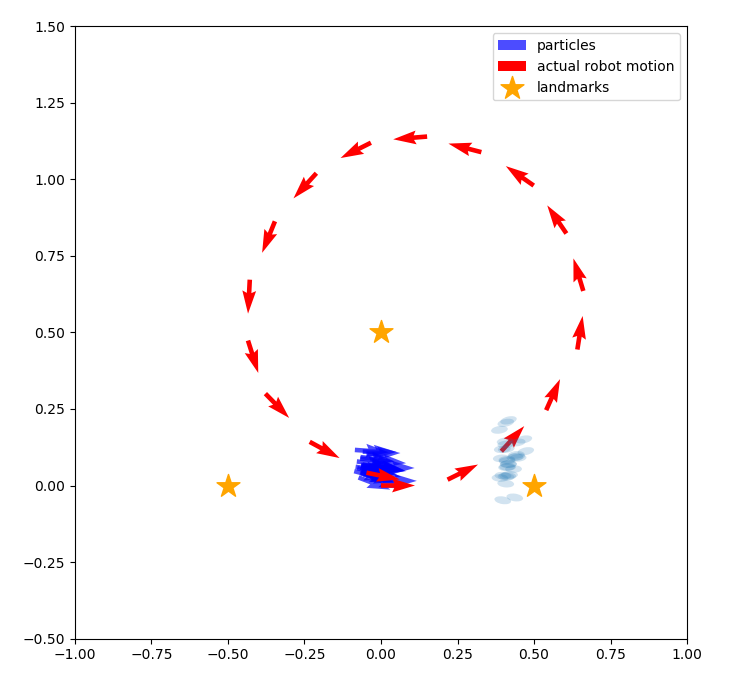
パーティクルフィルタよろしく,確率分布から取った複数のサンプル点でもって自らの信念を表示するわけですね。
matplotlibについて
今回ほぼはじめてPythonでまともなコード走らせるんですが,matplotlibというのも当然はじめてでして…
Referenceは以下になります。
pyplot — Matplotlib 2.0.2 documentation
基本的な流れは以下のような感じ?(pltとしてimportしてます。)
①figureハンドルを作成する。
.figureで以下のように図番号iとfigureサイズを指定してハンドルを作成するのでしょう。
fig = plt.figure(i,figsize=(8, 8))
②その後 figからなんかいろいろする。
普通にplt.~~でlineやcircleなど書けるようですが以下のプログラムではハンドル渡して.quiverなんかで矢印書いていますね
③表示 plt.show()
ここが少し不思議だったんですが一度作ったhandleは外でも生きているらしく,for文を抜けた後にまとめて表示してくれます。
matlabみたいにworkspaceを確認する手法があればわかりやすいのですが…spyderを使おう!(なおfigureハンドルは見えない模様)
コード
ほぼ全て上田先生の所にあったのをコピペしています。
これに適当にmcl1.pyとでも名前をつけて保存した後に実行するのが良いでしょう。
綺麗に書かれているのでこれを参考にしていろいろ書いて見ようかと思います。
#matplotlib inline import numpy as np from copy import copy import math, random import matplotlib.pyplot as plt # for plotting data from matplotlib.patches import Ellipse # for drawing class Gaussian2D: # 共分散行列、中心の座標を属性に持つ def __init__(self,sigma_x = 1.0, sigma_y = 1.0, cov_xy = 0.0,mu_x = 0.0, mu_y = 0.0): self.cov = np.array([[sigma_x**2,cov_xy],[cov_xy,sigma_y**2]]) self.mean = np.array([mu_x,mu_y]).T # ガウス分布の移動 def shift(self,delta,angle): ca = math.cos(angle) sa = math.sin(angle) rot = np.array([[ca,sa],[-sa,ca]]) self.cov = rot.dot(self.cov).dot(rot.T) self.mean = self.mean + delta # 密度の算出 def value(self, pos): delta = pos - self.mean numerator = math.exp(-0.5 * (delta.T).dot(np.linalg.inv(self.cov)).dot(delta)) denominator = 2 * math.pi * math.sqrt(np.linalg.det(self.cov)) return numerator / denominator class Landmarks: def __init__(self,array): self.positions = array def draw(self): xs = [ e[0] for e in self.positions] ys = [ e[1] for e in self.positions] plt.scatter(xs,ys,s=300,marker="*",label="landmarks",color="orange") class Observation: def __init__(self,robot_pos, landmark,lid): # センサの有効範囲の設定 self.sensor_max_range = 1.0 self.sensor_min_range = 0.1 self.sensor_max_angle = math.pi / 2 self.sensor_min_angle = - math.pi /2 # ランドマークのIDを保存しておく属性。ランドマークがセンサの有効範囲にないとNoneのまま self.lid = None # 真の位置の情報をセットする。ロボットの真の姿勢はシミュレーション用でロボットは知らないという前提。 # 真のランドマークの位置は、ロボットは知っているのでこのインスタンスの属性として保存します。 rx,ry,rt = robot_pos self.true_lx,self.true_ly = landmark # ロボットからランドマークまでの距離の真値を算出 distance = math.sqrt((rx-self.true_lx)**2 + (ry-self.true_ly)**2) if distance > self.sensor_max_range or distance < self.sensor_min_range: return # ロボットからランドマークがどの方向に見えるか真値を算出 direction = math.atan2(self.true_ly-ry, self.true_lx-rx) - rt if direction > math.pi: direction -= 2*math.pi if direction < -math.pi: direction += 2*math.pi if direction > self.sensor_max_angle or direction < self.sensor_min_angle: return # 真値に混入する雑音の大きさ(標準偏差)を設定 sigma_distance = distance * 0.1 # 距離に対して10%の標準偏差 sigma_direction = math.pi * 3 / 180 # ランドマークの方向に対して3degの標準偏差 # 雑音を混ぜてセンサの値とする self.distance = random.gauss(distance, sigma_distance) self.direction = random.gauss(direction, sigma_direction) # ロボット座標系での共分散行列を作っておく。あとで尤度を計算するときに使用 # x方向が奥行きで、sigma_distanceを標準偏差に設定。y方向がロボットから見て横方向の誤差で、距離*sin(3[deg])となる。 self.error_ellipse = Gaussian2D(sigma_x = sigma_distance, sigma_y = self.distance * math.sin(sigma_direction) , cov_xy = 0.0) self.lid = lid # 尤度の計算(遅い実装です。) # パーティクルの姿勢とランドマークの計測値からランドマークの位置を推定し、その位置に誤差楕円を置き、 # ランドマークの真の位置が誤差楕円からどれだけ外れているかを確率密度関数の密度として返します。 # この計算はもっと簡略化できますが、描画の関係でこういう手順を踏んでいます。 # 簡略な方法: パーティクルの姿勢とランドマークの真の位置から、想定されるランドマークの距離・方向を算出し、 # 実際の距離・方向とそれぞれ比較する方法。距離の誤差の傾向、方向の誤差の傾向をそれぞれ1次元のガウス分布で表現し、 # それぞれを独立して計算して尤度を算出し、掛け算する。 def likelihood(self,particle_pos): # パーティクルの姿勢と、このインスタンスに保存されているセンサの値から、ランドマークの位置を求める rx, ry, rt = particle_pos proposed_lx = rx + self.distance * math.cos(rt + self.direction) proposed_ly = ry + self.distance * math.sin(rt + self.direction) # このインスタンスに保存されている共分散行列を、計算されたランドマークの位置に移し、パーティクルの向きに合わせて共分散行列を回転 e = copy(self.error_ellipse) e.shift(np.array([proposed_lx, proposed_ly]).T, rt + self.direction) # そのままガウス分布の計算式から密度(尤度)を返します。 return e.value(np.array([self.true_lx,self.true_ly]).T) # 描画用 def ellipse(self,robot_pos): rx, ry, rt = robot_pos[0], robot_pos[1], robot_pos[2] proposed_lx = rx + self.distance * math.cos(rt + self.direction) proposed_ly = ry + self.distance * math.sin(rt + self.direction) e = copy(self.error_ellipse) e.shift(np.array([proposed_lx, proposed_ly]).T, rt + self.direction) # 固有ベクトルを二つ求めて、それぞれの大きさを求めて楕円を作り、幅を計算した方の固有ベクトルの向きに楕円を回転すると誤差楕円になります。 eigen = np.linalg.eig(e.cov) v1 = eigen[0][0] * eigen[1][0] v2 = eigen[0][1] * eigen[1][1] v1_direction = math.atan2(v1[1],v1[0]) elli = Ellipse([proposed_lx, proposed_ly],width=math.sqrt(np.linalg.norm(v1)),height=math.sqrt(np.linalg.norm(v2)),angle=v1_direction/3.14*180) elli.set_alpha(0.2) return elli # 描画用 def draw(self,sp,robot_pos): sp.add_artist(self.ellipse(robot_pos)) actual_landmarks = Landmarks(np.array([[-0.5,0.0],[0.5,0.0],[0.0,0.5]])) actual_landmarks.draw() # パーティクルのクラス。単なる構造体 class Particle: def __init__(self,x,y,t,w): self.pos = np.array([x,y,t]) self.w = w # パーティクルフィルタのクラス class ParticleFilter: # この実装ではコンストラクタはパーティクルの個数だけを引数にとる def __init__(self,num): # 空のパーティクルのリストを作って一つずつ追加していく(実装がベタ) self.particles = [] for i in range(num): self.particles.append(Particle(0.0,0.0,0.0,1.0/num)) # パーティクルは重みを持つ。全パーティクルの重みの合計は1。1つのパーティクルの重みは1/個数 # ロボットが動いたときにパーティクルを動かすためのメソッド # 引数の「motion」はメソッドで、ロボットの移動を再現するためのもの。 # ロボットは自身がどのように動作するとどう姿勢が変化するかを知っており、このメソッドがその知識となる。 def moveParticles(self,fw,rot,motion): self.resampling() # このメソッドについては後述 # パーティクルごとに移動した後の姿勢を計算し、姿勢を更新する。 for p in self.particles: after = motion(p.pos,fw,rot) p.pos = after # リサンプリングのためのメソッド。 # リサンプリングは、重みがごく少数のパーティクルに偏ることを防ぐための措置で、近似していない理論上の数式では出現しない。 def resampling(self): num = len(self.particles) # numはパーティクルの個数 ws = [e.w for e in self.particles] # 重みのリストを作る print(sum(ws)) if sum(ws) < 1e-100: #重みの和がゼロに丸め込まれるとサンプリングできなくなるので小さな数を足しておく ws = [e + 1e-100 for e in ws] ps = random.choices(self.particles, weights=ws, k=num) # パーティクルのリストから、weightsのリストの重みに比例した確率で、num個選ぶ self.particles = [Particle(*e.pos,1.0/num) for e in ps] # 選んだリストからパーティクルを取り出し、パーティクルの姿勢から重み1/numの新しいパーティクルを作成 # 描画用 def draw(self,c="blue",lbl="particles"): xs = [p.pos[0] for p in self.particles] ys = [p.pos[1] for p in self.particles] vxs = [math.cos(p.pos[2]) for p in self.particles] vys = [math.sin(p.pos[2]) for p in self.particles] plt.quiver(xs,ys,vxs,vys,color=c,label=lbl,alpha=0.7) class Robot: def __init__(self,x,y,rad): random.seed() # actual_poses: ロボットの姿勢の真値を1ステップごとに記録したもの # (ロボットのクラス内にいるけどロボットはこの情報を使えない) self.actual_poses = [np.array([x,y,rad])] # パーティクルフィルタの準備(パーティクル数30個) self.pf = ParticleFilter(30) # ロボットの動作をシミュレートするメソッド。シミュレーションだけでなく、ロボットがパーティクルを移動するときにも用いる。 # つまり実機に実装する場合もこのメソッドが必要となる。雑音の度合いは事前に計測するか、 # ざっくり決めてフィルタのロバスト性に頼る。 def motion(self, pos, fw, rot): # fwだけ前進してその後rotだけ回転。雑音を混入させる actual_fw = random.gauss(fw,fw/10) #進む距離に対して標準偏差10%の雑音を混入 dir_error = random.gauss(0.0, math.pi / 180.0 * 3.0) # 前進方向がヨレる雑音を標準偏差3[deg]で混入 px, py, pt = pos # 移動後の位置を算出 x = px + actual_fw * math.cos(pt + dir_error) y = py + actual_fw * math.sin(pt + dir_error) # 雑音込みの回転各を算出。rotに対して標準偏差10%の雑音を混ぜる actual_rot = random.gauss(rot,rot/10) t = pt + dir_error + actual_rot # さらにヨレの分の角度を足す return np.array([x,y,t]) # ロボットが動くときに呼び出すメソッド。ロボットの位置の更新とパーティクルの位置の更新 def move(self,fw,rot): self.actual_poses.append(self.motion(self.actual_poses[-1],fw,rot)) self.pf.moveParticles(fw,rot,self.motion) # ロボットがランドマーク観測するときに呼び出すメソッド def observation(self,landmarks): obss = [] for i,landmark in enumerate(landmarks.positions): # 3つあるランドマークを1つずつ観測 obss.append(Observation(self.actual_poses[-1],landmark,i)) obss = list(filter(lambda e : e.lid != None, obss)) # 観測データのないものを除去 # 重みに尤度をかける for obs in obss: for p in self.pf.particles: p.w *= obs.likelihood(p.pos) # 描画用に観測のリストを返す return obss # 描画用 def draw(self,sp,observations): for obs in observations: for p in self.pf.particles: obs.draw(sp,p.pos) self.pf.draw() xs = [e[0] for e in self.actual_poses] ys = [e[1] for e in self.actual_poses] vxs = [math.cos(e[2]) for e in self.actual_poses] vys = [math.sin(e[2]) for e in self.actual_poses] plt.quiver(xs,ys,vxs,vys,color="red",label="actual robot motion") def draw(i,observations): fig = plt.figure(i,figsize=(8, 8)) sp = fig.add_subplot(111, aspect='equal') sp.set_xlim(-1.0,1.0) sp.set_ylim(-0.5,1.5) robot.draw(sp,observations) actual_landmarks.draw() plt.legend() robot = Robot(0,0,0) # ロボットを原点に # 観測、描画、移動の繰り返し for i in range(0,18): obss = robot.observation(actual_landmarks) draw(i,obss) robot.move(0.2,math.pi / 180.0 * 20) plt.show()
お言葉
最後に講演で先生がおっしゃった言葉で,
「便利なツールがあるなら使ってください。勉強以外の目的で自分で組むのはおすすめしません。」
というのが印象に残っています。
殊,Pythonに関しては情報にアクセスさえできればツールは使えますもんね。
情強になりたい…