粗大メモ置き場

個人用，たまーに来訪者を意識する雑記メモ

カルマンフィルタの推定値の信頼区間を書く

MATLAB

カルマンフィルタから信頼区間の線を引きたいというのは当然の要求だと思うのですが見渡す限り 良さげな文献が無いので自分で書きます。 書いておいて何ですが自信がないので訂正等のご意見を随時求めております。

あと，ブログの本文もMarkdownにシフトしてみました。
[tex: ]ってうつのめんどくさいな。

理論

参考文献

きちんとした参考文献を見つけられずに困ってます。 一番まともそうなのがStackOverflowしかないんだけど… python - Estimating confidence intervals around Kalman filter - Stack Overflow

あと，確率論とかについては以下の本を。

確率ロボティクス (プレミアムブックス版)

確率ロボティクス (プレミアムブックス版)

足立先生の本も良著なのでオススメ。
カルマンフィルタの基礎

カルマンフィルタの基礎

追記：それっぽい論文見つけました1966年の論文です。 Confidence, Prediction, and Tolerance Regions for the Multivariate Normal Distribution on JSTOR

カルマンフィルタにおける信頼区間とは

まずは信頼区間についてwikiで確認してください。 信頼区間 - Wikipedia

以下の図のように分布の形状と平均分散などの値がわかっていれば値がどの確率でどの範囲に収まっているかがわかります。 こういうやつ

カルマンフィルタでは誤差にガウス分布を仮定しており，我々がフィルタで推定する推定値Xはこの分布の平均値でした。 また，この際同時に誤差共分散行列Pも求められるので推定値の不確かさも同時に推定できます。

従ってこれらの情報からある値の範囲に真値がN%の確率で存在するだろうということがわかります。

n次の状態変数における信頼区間

追記：上記の論文から記述を引っ張ってきました。 f:id:ossyaritoori:20171121163838p:plain

さっくり要約すると推定値\bar{x}と推定共分散行列Pに対して，αの信頼区間を示す楕円は次のように計算できるというものです。
(x-\bar{x})^\top P^{-1} (x-\bar{x}) = \chi ^2 (1-\alpha,n)

カイ二乗分布で検定できるんですね。 カイ二乗分布 - Wikipedia

別解：シグマ区間からの拡張

StackOverflowの記述によると以下の方程式を解くことでベクトルxに対する1シグマの区間を計算できます。 これの出典が知りたい…

(x-\bar{x})^\top P^{-1} (x-\bar{x}) = 1 ここから１σ区間を推定してカイ二乗分布から何σ分の信頼区間が必要になるのかを推定して何倍かすれば求まるでしょう。

Matlabによる実装１

とりあえず，論文にあった手法を実装してみましょう。SymbolicMath ToolBoxが必要になります。

カイ二乗分布の境界値

要は \chi ^2 (1-\alpha,n)を計算します。 一応以下のような表があるのですが，matlabではchi2inv(α,n)という関数が用意されています。 付表：カイ2乗分布表 chi-square distribution — 中川雅央（滋賀大学） カイ二乗逆累積分布関数と言うらしいですね。 試しに，2自由度の95%信頼区間が何σ必要かという話では

chi2inv(0.95,2)

とうつと5.9915と計算できます。

統計の授業でやる1自由度の時の1σ区間に68.27%のデータが入っているという話は chi2inv(0.6827,1)＝１という結果から確認できます。 注意として1自由度の時の2σ区間には95.5%の値が入っていますが chi2inv(0.955,1)=4.0186の結果からわかるように 逆累積分布関数から計算されるのは区間の大きさの2乗です。（用語が不明瞭）

Symbolic Math Toolboxを用いた代数方程式の解法

MATLABのStudentにデフォルトで入っているSymbolicMathToolboxを使えば次のような式はいとも簡単に解くことが可能です。 ２自由度までならせいぜい扁平な楕円なので頑張って手計算するというのも良いかもしれませんが。 (x-\bar{x})^\top P^{-1} (x-\bar{x}) = \chi ^2 (1-\alpha,n)

具体的な例で行きましょう。

% Set Value
Xhat = [1;2]
Phat =[1 0.5;0.5 2]

% Get dimension
Dim = size(Xhat,1);
alpha = 0.95;
bound = chi2inv(alpha,Dim);

% Set symbolic equation
X = sym('x',[Dim 1]);
equation = (X-Xhat).'*inv(Phat) *(X-Xhat) == bound

% Plot Function
ezplot(equation)
hold on 
plot(Xhat(1),Xhat(2),'r+')
grid on

今回得た知見として，ezplotを用いることでEquationをplotできるのが簡単で良さげです。 f:id:ossyaritoori:20171121173519p:plain

SLAMなどではこのまま楕円の範囲が位置推定の信頼区間になるのでいいですが，カルマンフィルタの状態推定の場合各状態の変位の範囲が知りたいわけなので， 以下の青線の範囲が知りたいわけです。 f:id:ossyaritoori:20171121174056p:plain

これは先程のEquationに状態変数の値を代入して解くことで達成されて，

Eq1 = subs(equation,X(2),Xhat(2));
Eq2 = subs(equation,X(1),Xhat(1));

Ans1=double(solve(Eq1));
Ans2=double(solve(Eq2));

結果，次のようになります。これが知りたかった95%信頼区間の下界と上界です。

Ans1 =

   -1.2897
    3.2897

Ans2 =

   -1.2381
    5.2381

実は，結局ある状態変数の信頼区間の上界下界の計算に必要なのは共分散行列の逆行列のi行i列目の成分だけなのです。 もっと言うと，共分散行列の逆行列の逆数の値がその推定値の標準偏差になるってところでしょうか。

MATLAB関数として実装

関数として書こうと思ったんですが先程の流れをそのまま関数にすると結構重いものが出来上がります。 とりあえずConfidenceInterval.m関数を作成しました。

実際に適用すると例えばこんな感じ。正直大げさなくらいの範囲が求まります。 f:id:ossyaritoori:20171121223208p:plain

引数は推定値，共分散行列，信頼区間(デフォルト値95%)です。 要望やバグがあればブラッシュアップします。

追記＆最終版：実は超簡単

上記の関数は問題をややこしく解いています。 楕円を書かなくても良い場合，実は問題は超簡単で 以下の数式を解けば良いことになります。 f:id:ossyaritoori:20171121232247p:plain

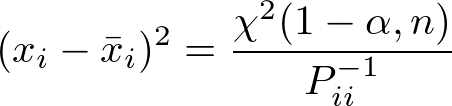
おそらく改善の余地がないのでこれを最終版とします，

% Author: Yoshi Ri @ The Univ of Tokyo 
% Date : Nov 2017
% Get ConfidenceInterval of 

function [Xmax ,Xmin]= ConfidenceInterval(Xhat,Phat,p)
% Xhat : Estimated State, Phat : Estimated Covariance, p : percentage of
% prediction

if nargin==2
p=0.95;
%print('set default p=95%!')
end

% Get dimension
Dim = size(Xhat,1);
alpha = p;
bound = chi2inv(alpha,Dim);

% Set symbolic equation
Pinv= inv(Phat);

% Get upper and lower boundary
Xmax=zeros(size(Xhat));
Xmin=zeros(size(Xhat));
for i=1:Dim
    Xmin(i)=Xhat(i)- sqrt(bound/Pinv(i,i));
    Xmax(i)=Xhat(i)+ sqrt(bound/Pinv(i,i));
end

end

疑問点

そもそも筆者は検定とか統計とかふわふわした知識でやっているので， 強マンによる本質的な記事の矯正が必要です。

心が折れない程度に指摘してください。