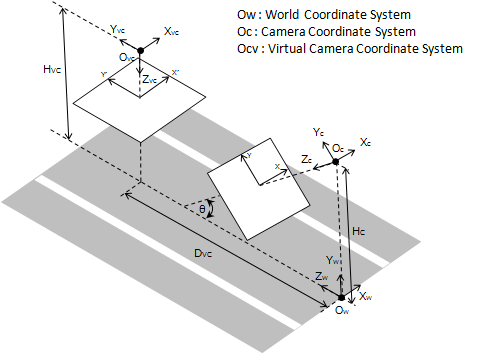
ホモグラフィー行列を用いた鳥瞰変換(Bird's-eye view)
鳥瞰変換とは
一言で言うと,ある視点からとったカメラの画像を別の視点で撮ったように見せかける手法のことです。
他サイト様の説明がわかりやすいのでこちらに載せます。 daily-tech.hatenablog.com
より一般的には「斜めから撮った画像を真上から撮った画像のように写す」という場面で使われます。
鳥瞰変換とホモグラフィー変換
カメラの撮像の式
グローバル座標系にて座標にある点をカメラの位置①から撮像して画像上の点
に写っているとします。
今,仮想的なカメラの回転
を施した系②でこれが
に移るとします。(この系②が上から見下ろす系になっていればいいわけですね。)
それぞれの場合でのカメラの撮像の式は以下のようになります。(Texで打ったので画像で失礼)

ホモグラフィー変換
一方,画像変換で用いられるホモグラフィー変換はホモグラフィー行列を用いて次のような形で表せます。

カメラの回転とホモグラフィー変換の関係性
上のニ式を見比べてみると,回転行列と
との間には以下のような直接対応関係があることがわかります。
当然ですが,系①と②の間に純粋な回転以外の並進成分などがあった場合はこんな簡単な関係にはなりません。

この関係を用いることでカメラを擬似的に真下向きに回したときの画像を生成することができるというわけです。
おまけ:手ぶれ補正
先程の式は裏を返せば,微小な並進成分を無視すれば画像内のホモグラフィー変換からカメラの回転を補正することができるということを表しています。 この手法を用いて手ぶれ補正をしたのが以下の記事だったりするわけです。
実践編
例のごとくOpenCVを使います。
下準備
先程の式を用いて鳥瞰変換を行う際には以下のパラメータが必要になります。
- カメラ行列K
- 系①におけるカメラ姿勢(R,t)(→ 実はRだけでいい)
これは一般にキャリブレーションと言われる作業です。
Ubuntu-ROS環境が整っている方にとっては造作もないと思いますが,Windowsなどでやる場合は下記のサイト等でやるのが良いかと思います。 ossyaritoori.hatenablog.com
また,カメラ姿勢(R,t)を測るのは結構大変で,ARマーカ等を用いるのが最も楽かなぁという気がします。 プログラムは適当に探してもらうとして,この辺りの記事なんかが説明が簡素でわかりやすいかも?
プログラムの流れ
カメラの姿勢Rの元となるrvecから座標系①における回転を計算します。
ossyaritoori.hatenablog.com
また,変換したい座標系②での回転を
cv2.Rodriguesから生成しておきます。
この時,先程のと計算できます。
その後,Kをかけて作ったホモグラフィー行列を元に
cv2.warpPerspectiveに投げます。以上です。
略記プログラム
コードメモですがこのままでは動きませんよ~
# calculate bird view homography import math theta_below = np.array([0, math.pi, 0]) Rc_, _ = cv2.Rodrigues(theta_below)#変換先の回転 Rc,_ = cv2.Rodrigues(vm.rvecs)#オリジナル関数有 Homo = np.linalg.multi_dot([K,Rc_.T,Rc.T,np.linalg.inv(K)])#ホモグラフィー行列 nHomo = Homo/Homo[2,2]# 正規化 minx = -20000 miny = 0 # 移動量を調整しないと画面外に出ていってしまう… nHomo[0,2] -= minx nHomo[1,2] -= miny # 2000pix四方の画面を用意しないとどっか行っちゃうので… out=cv2.warpPerspective(img,nHomo,(2000,2000))