オドメトリを連結している別の座標系に移す時の座標変換計算（ROS）

概要
tfを使った解法
自分で計算するときの数式
まとめ
参考文献

概要

下記のようなシチュエーションのオドメトリ変換を考えます。

Bodyに固定したセンサでとったodometryをbase_linkでのオドメトリに変換するのが目的です。（ROSでよくあるシチュエーションだと思います。）

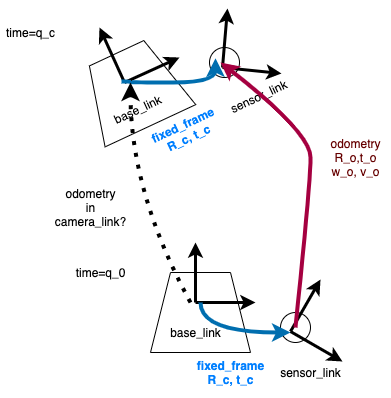
f:id:ossyaritoori:20210828003827p:plain

注意：速度変換の部分に自信がないです。詳しい方訂正・コメントお願いします。

tfを使った解法

ROSを使う人なら位置変換に関しては普通にROSのtfを

/base_link(q_0) -> /sensor_frame(q_0) -> /sensor_frame(q_c) -> /base_link(q_c)

のような感じでつないでlookupTransformで解決すれば位置の変換が取得できるとお思いになるかと思います。一方で、速度（twist）の解決は私の知る限りサポートされていないように思います。

一応、lookupTwistというのがあるのですがこれはlookupTransformの結果を数値微分しているっぽいのであまり正確な値は期待できません。

また、複数のセンサがある場合などは複数の経路ができてtf treeの構造を壊しかねないのでエスケープのために余計なリンクをたくさん定義することになります。

自分で計算するときの数式

以上の課題を解決するために自分で計算していきます。

位置の変換

同次行列をつないでいけば、base_linkの座標系で見たOdometryのPoseは

$\displaystyle \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} R_c & t_c \\ 0 & 1 \end{bmatrix}\begin{bmatrix} R_o & t_o \\ 0 & 1 \end{bmatrix}\begin{bmatrix} R_c & t_c \\ 0 & 1 \end{bmatrix}^{-1}$

で計算できます。これを全て計算すると下記のようになります。

$\displaystyle \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} R_c R_o R_c ^\top & -R_c R_o R_c ^\top t_c + t_c + R_c t_o \\ 0 & 1 \end{bmatrix}$

ここで、 $R_o,R_c$ が可換の時、具体的にはyaw回転しかしない自動車などのアプリケーションでカメラを水平に構えた時などは

$\displaystyle \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} R_o & - R_o t_c + t_c + R_c t_o \\ 0 & 1 \end{bmatrix} \mbox{(R_oとR_c が可換のケース)}$

とすることができます。

どこかが違うtwistの変換（Pose変換の微分で解く）

~~Poseの変換がわかったので上記の式を時刻qで微分することで、Twist変換に変換することができます。（よね？）~~

なんか上記の仮定が間違っている気がしてきました。一応途中式は残しておきます。結果が少し異なるのですが何が違うのかちょっと自信がないので

何かがおかしい気がする導出

記述量削減のため $\frac{dR_x}{dq} = \tilde{\omega_x} R_x, \frac{dt_x}{dq} = v_x$ と記述することにします。ここで $\omega_x$ は角速度で、 $\tilde{\omega_x}$ はその交代行列です。この辺の話は面白いのでぜひ参考文献をご覧あれ。

$R_o,t_o$ のみが時変なので微分は下記のように計算できます。

$\displaystyle \begin{bmatrix} \tilde{\omega} R & v \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} R_c \tilde{\omega_o} R_o R_c ^\top & -R_c \tilde{\omega_o} R_o R_c ^\top t_c + R_c v_o \\ 0 & 1 \end{bmatrix}$

角度の関係は

$\displaystyle \tilde{\omega} R = \tilde{\omega} R_c R_o R_c ^\top =R_c \tilde{\omega_o} R_o R_c ^\top$

を解いて

$\displaystyle \tilde{\omega} =R_c \tilde{\omega_o} R_c^\top$

となります。角速度の関係は参考文献[2]から $\omega = R_c \omega_o$ と簡単な形に求まります。

並進速度は下記の感じになります。

$\displaystyle v = -R_c \tilde{\omega_o} R_o R_c ^\top t_c + R_c v_o$

また、R_o R_c が可換のケースでは下記のようになります。

$\displaystyle \tilde{\omega} = \tilde{\omega_o} \\ v = - \tilde{\omega} R t_c + R_c v_o \\ \mbox{(R_o R_c が可換のケース)}$

並進速度の第一項は回転に伴うモーメントのような項ですね。

twistの変換（多分こっちが正しい。）

twist（速度・加速度）の変換に自信がなく結構調べたのですが調べる際によく出る例として下記の質疑があります。参考文献[4]のスライドがいい感じだと思われます。

physics.stackexchange.com

要約すると座標Aで見た速度を座標A'で見たときにどうなるかを表す式は

$\displaystyle \begin{pmatrix} v_{A'} \\ \omega_{A'} \end{pmatrix} = \begin{pmatrix} R_{A'A} & \hat{t}_{A'A}R_{A'A} \\ 0 & R_{A'A} \end{pmatrix} \begin{pmatrix} v_{A} \\ \omega_{A} \end{pmatrix}$

とかけるというものです。

自分の変数に書き下すと下記の通りになります。vは並進tを時間微分したものです。

$\displaystyle \begin{pmatrix} v \\ \omega \end{pmatrix} = \begin{pmatrix} R_c & \tilde{t}_cR_c \\ 0 & R_c \end{pmatrix} \begin{pmatrix} v_{o} \\ \omega_{o} \end{pmatrix}$

ここで、 $\tilde{\omega}$ は角速度ベクトルの交代行列であり、 $\dot{R_x} = \tilde{\omega_x} R_x$ のように微小回転行列を表せます。この辺は結構面白いのでリー代数や三次元回転についての記述を参照してください。（参考文献1）

展開すると並進速度は外積の性質などを用いて、

$\displaystyle v = \tilde{t}_cR_c \omega_o + R_c v_o\\ = t_c \times R_c \omega_o + R_c v_o\\ = - \omega \times t_c + R_c v_o\\ = - \tilde{\omega} t_c + R_c v_o$

とかけます。

導出

導出の元になる数式は下記のようになっています。

$\displaystyle \begin{bmatrix} \tilde{\omega} & v \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} R_c & t_c \\ 0 & 1 \end{bmatrix}\begin{bmatrix} \tilde{\omega}_o & v_o \\ 0 & 1 \end{bmatrix}\begin{bmatrix} R_c & t_c \\ 0 & 1 \end{bmatrix}^{-1}$

角度について展開すると

$\displaystyle \tilde{\omega} =R_c \tilde{\omega_o} R_c^\top$

となります。角速度の関係は参考文献[2]から $\omega = R_c \omega_o$ と簡単な形に求まります。

並進速度は下記のように書けます。

$\displaystyle v = -R_c \tilde{\omega_o} R_c ^\top t_c + R_c v_o = -\tilde{\omega} t_c + R_c v_o$

補足

交代行列について

$\omega = \begin{bmatrix} r , p , y \end{bmatrix} ^\top$ の時、

$\displaystyle \tilde{\omega} = \begin{bmatrix} 0 & -y & p\\ y & 0 & -r\\ -p & r &0 \end{bmatrix}$

この行列は下記の性質を持ちます。

$\displaystyle \tilde{\omega}^\top = - \tilde{\omega}$

$\omega = R_c \omega_o$ の導出

スマートな解釈としては参考文献[3]の式（8）あたりを見てもらうと良いですが、実は以下の2式をゴリゴリ成分計算することでも求まります。

$\displaystyle \tilde{\omega} =R_c \tilde{\omega_o} R_c^\top$

f:id:ossyaritoori:20210828131106p:plain — rpyの角度から算出する三次元回転行列（'sxyz'）

まとめ

ということで機体から $R_c,t_c$ の位置に取り付けられたセンサのオドメトリ $R_o,t_o,\omega_o,t_o$ から得られる機体のオドメトリ $R,t$ は

$\displaystyle R = R_c R_o R_c ^\top \\ t = -R_c R_o R_c ^\top t_c + t_c + R_c t_o \hspace{5mm}= -R t_c + t_c + R_c t_o\\ \omega =R_c \omega_o \\ v = -R_c \tilde{\omega_o} R_c ^\top t_c + R_c v_o \hspace{5mm} = - \tilde{\omega} t_c + R_c v_o$